「正比例に近い整数による配分」$\left( A; d \right)$、ただし、$d:=\left( d_1, \ldots, d_n \right)$とは?配分すべきものが$A$個あり、$n$人のプレイヤーの要求量はベクトル$d=\left( d_1, \ldots, d_n \right)$で表される。$A$個をなるべく$d$に正比例になるように整数値で分ける、のが問題である。
$\left( A; d \right)$、ただし、$A=9, d=\left( 2,4,5,7 \right)$のウェブスター法による解を優先法と除数法によって求める。この問題には2通りの解がある。
優先法
まず、優先法で求める。
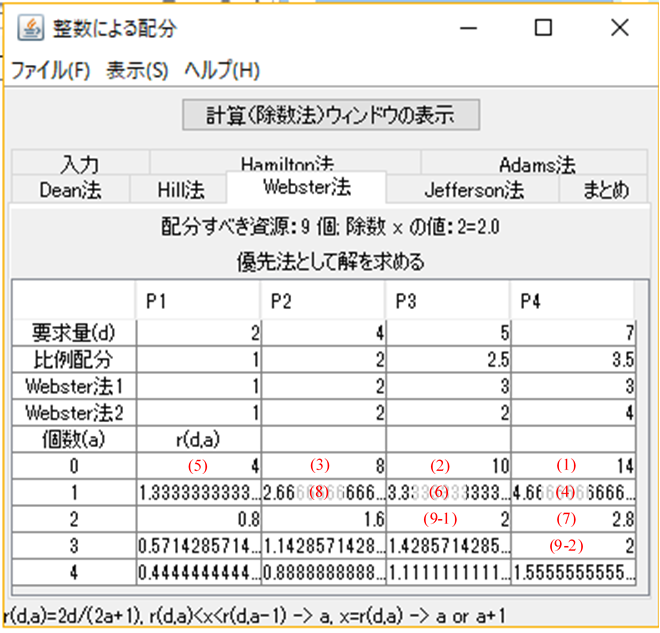
上図を参照する。優先度の高い順に9個選ぶと、(1)$14$、(2)$10$、(3)$8$、(4)$4.6\cdots$、(5)$4$、(6)$3.3\cdots$、(7)$2.8$、(8)$2.6\cdots$、の8個と、9個目の$2$((9-1)と(9-2)の2個ある)となり、${\rm Web}=\left( 1,2,3,3 \right), \left( 1,2,2,4 \right)$の2通りとなる。
除数法
次に、除数法で求める。
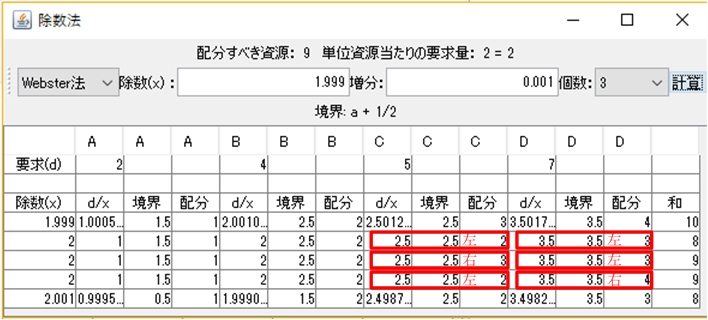
上図を参照する。除数$x$が$2$より少し小さい時、$\left( 1,2,3,4 \right)$の$10$個が必要で、$x$が$2$より少し大きい時、$\left( 1,2,2,3 \right)$の$8$個が必要である。$x$がちょうど$2$の時、2人のプレイヤー${\rm P}_3$(C)と${\rm P}_4$(D)の$d/x$が境界上にあり、小さい方に丸めても大きい方に丸めてもどちらでもよい。従って、和がちょうど$9$になるように一方を小さい方へ他方を大きい方へ丸めて、${\rm Web}=\left( 1,2,3,3 \right), \left( 1,2,2,4 \right)$の2通りとなる。この例では、除数法で解を求める場合、除数$x$が一意に$2$と決まった。