Monty Hall Problem が Ken Binmore 著「Game Theory: A Very Short Introduction」の第10章に紹介されている。興味を持ったので、少し詳しく述べる。
Monty Hall Problem
箱1、箱2、箱3の3つがあり、そのうちの1つに賞金が入っている。貴方は賞金が入っている箱を当てたい。Monty は賞金がどの箱に入っているかを知っていて、参加者である貴方は知らない。まず、貴方が箱を選び、その次に Monty が他の2つの箱から賞金が入っていない箱を選び、その箱を開いて実際に賞金が入っていないことを示す。その時、貴方は最初に選んだ箱を変えない、または、箱を変える、のどちらかに決めることが出来る。例えば、貴方が箱2を選び、その後、Monty が箱3を開いて賞金が入っていないことを示したとする。その時、貴方は
- 自分の最初の選択(この場合は、箱2を選ぶ)を変えない。(この決定を「維持」と呼ぶことにする。)
- 自分の最初の選択を(この場合は箱1を選ぶに)変える。(この決定を「変更」と呼ぶことにする。)
どちらの決定をすべきであろうか?
答えは、2.である。何故そうなるか?の理由を述べるのが今回の目的である。
数理的に扱いやすいようにこの問題を貴方と Monty の2人ゼロ和ゲームとして整理する。
問題の定式化
- 箱1、箱2、箱3の3つのがある。自然がランダムに選んだ箱に賞金が入っている。貴方はどの箱に賞金が入っているか知らないので、箱$i(i=1,2,3)$に賞金が入っている確率は$\frac{1}{3}$である、と見積もっている。一方、Monty は自然が選んだ箱を知っている、すなわち、どの箱に賞金が入っているかを知っている。
- 貴方は自分の意思で箱1、箱2、箱3から1つの箱を選ぶ。
- Monty は、どの箱に賞金が入っているか知っているので、貴方が選んだ箱以外の2個の箱から賞金の入っていない方を選び、その箱を開いて賞金が入っていないことを示す。
- 貴方は、(1)B.で選んだ箱を「維持」し、最終的な決定とする。(2)B.で選んだ箱を「変更」し、最終的な決定を、C.でMonty も選んでいない残りの箱にする。
- 貴方が最終的に決定した箱に賞金が入っていれば、貴方の「勝ち」で利得として賞金1を Monty から貰う、そうでなければ、貴方の「負け」で利得の授受はない、とする。
- 貴方は貴方の利得を大きくしたい。Monty は貴方の利得を小さくしたい。自然がランダムに箱を選ぶので、結局、貴方は貴方の利得の期待値(勝つ確率)を大きくしたい。Monty は貴方の利得の期待値(勝つ確率)を小さくしたい。
この2人ゼロ和ゲームの答え、貴方と Monty の最適戦略とゲームの値は次のようになる。
貴方の最適戦略:
B.では、どの箱を選んでもよい。特に、箱1、箱2、箱3を、各々、$\frac{1}{3}$の確率で、すなわち、ランダムに選ぶ。D.では、(2)の「変更」を選ぶ。Monty の最適戦略:
C.では、貴方が選んでいない、かつ、賞金が入っていない、どの箱を選んでもよい。特に、貴方が賞金の入っている箱を選んだ場合、残りの2つの箱を、各々、$\frac{1}{2}$の確率で、すなわち、ランダムに選ぶ。ゲームの値は$\frac{2}{3}$である。
まず、直感的に考える。
(1)貴方がD.で「維持」を選ぶと仮定する。この時、貴方が勝つ確率はB.で賞金の入っている箱を選ぶ確率と等しい。B.で箱1、箱2、箱3、を選ぶ確率を、各々、$p_1$、$p_2$、$p_3$とすると、この勝つ確率は$p_1 \frac{1}{3} + p_2 \frac{1}{3} + p_3 \frac{1}{3} = \frac{1}{3}$となる。
(2)貴方がD.で「変更」を選ぶと仮定する。貴方がB.で賞金の入っている箱を選ぶと、結果は負けとなる。貴方がB.で賞金の入っていない箱を選ぶと、(Monty はC.で賞金の入っていないもう1つの箱を開けるので、残りの箱には賞金が入っている。従って、)結果は勝ちとなる。すなわち、貴方がB.で賞金の入っていない箱を選ぶと、結局勝つことになる。(1)と同様に考えて、この時の勝つ確率は$\frac{2}{3}$となる。
以上より、「維持」の勝率は$\frac{1}{3}$、「変更」の勝率は$\frac{2}{3}$であり、従って、B.では(2)の「変更」を選ぶ。
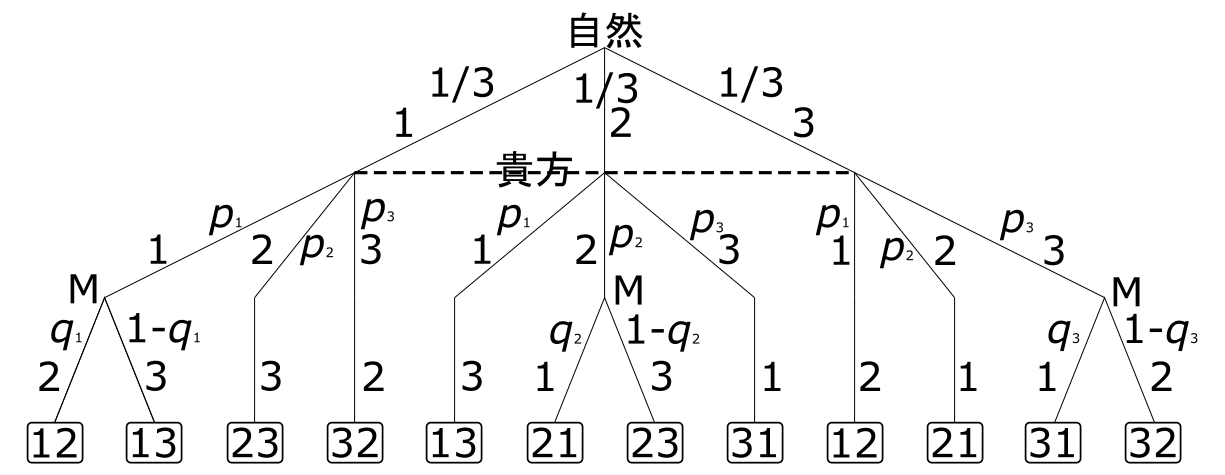
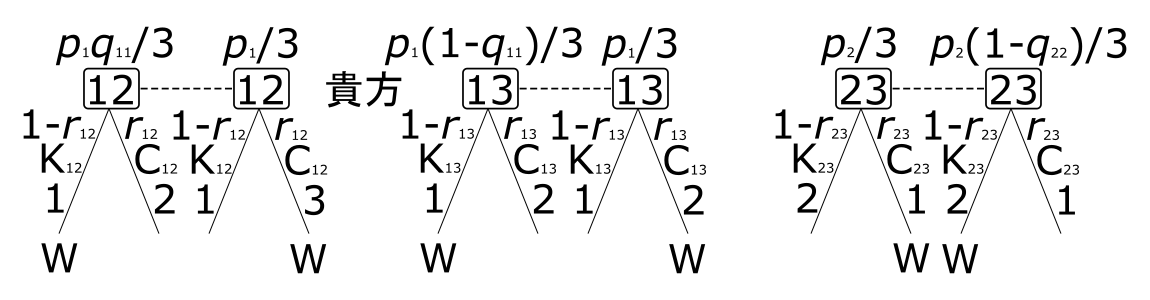
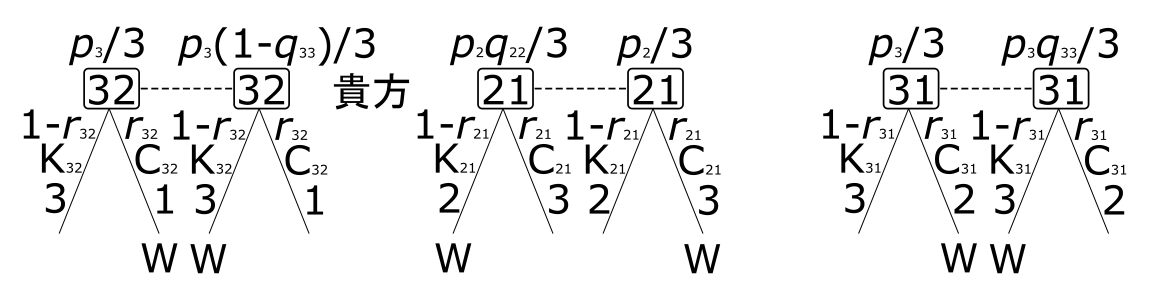
次に、ゲームの木を書いて、明示的に、2人ゼロ和ゲームとして捉え、それを解いてみる。ゲームの木が大きすぎるので3つ(ゲームの木1、ゲームの木2、ゲームの木3)に分割して書いてある。まず、自然がゲームの木1の一番上の「自然」と書かれたノード(手番、自然がランダムにとるので偶然手番、と呼ばれる)で賞金を入れる箱を選ぶ。確率$\frac{1}{3}$ずつで、箱1、2、3を選ぶ。次は、貴方の手番で、貴方は自然が選んだ箱を知らずに、箱1、2、3を選ぶ。貴方が自然が選んだ箱を知らないことを示すために、自然が選んだ箱1、2、3を表すノードを破線で結んであり、この3つのノードのどれかにいることは知っているがどれにいるかは知らないことを表し、この3つのノードからなる集合は情報集合と呼ばれている。次の手番は Monty である。Monty は自然が選んだ箱も貴方が選んだ箱も知っているので、9個のノードのどれにいるか正確に知っている。Monty の役割は貴方が選んでいない、かつ、賞金が入っていない、箱を開けるので、貴方が賞金が入っていない箱を選んだ場合、Monty が開ける箱は決まっている。貴方が賞金の入っている箱を選んだ場合、Monty は残りの2つの箱から1個を選ぶ必要があるので、そのノードに M と書いてある。この3つのノードにおいて、Monty は左か右を選ぶ。例えば、M と書いてある一番左のノードでは左は Monty が箱2を、右は Monty が箱3を開けることを意味する。以上で、ゲームの木1の一番下の、2桁の数字が書かれた12個のノードの所までゲームが進んだ。例えば、12は貴方が最初の手番で箱1を選び、Monty が箱2を開けたことを意味する。貴方は自然が選んだ箱を知らないので、この12個のノードの中で、一番左にある12と書かれたノードと右から4個目にある12と書かれたノードを区別できない、従って、この2つは情報集合をなし、12と表記する。従って、6個の情報集合、12、13、21、23、31、32、があることになり、これらの貴方の2番目の手番以降の部分を書いたのが、ゲームの木2とゲームの木3)である。
左は最初の手番の選択を維持(Keep)することを意味し、右は最初の手番の決定を変更(change)することを意味する。一番下で、W と書かれたノードでは、貴方が賞金の入っている箱を当てた(勝った)ので貴方が Monty から利得1を貰い、何も書かれていないノードでは、利得の授受はない。
以上で、ゲームの木(このゲームの展開形による表現)の説明は終わった。通常のゲーム理論の教科書では、この展開形表現から戦略形を求め、それを基に、両プレイヤーの最適戦略(貴方のマックスミニ戦略と Monty のミニマックス戦略)とゲームの値を求めるのであるが、後で分かるように、貴方と Monty の純粋戦略の個数が、各々、192個と8個なので、戦略形(ここでは、192行8列の利得表を書くこと)を扱うのは困難なので、まず、行動戦略を考え、それを基にこの2人ゼロ和ゲームを解き、最後に、混合戦略と行動戦略の関係に言及する。
さて、行動戦略とは、自分の手番になった時、そこでの手を確率的に選ぶことである。貴方の行動戦略は、最初の手番で箱1、箱2、箱3を選ぶ確率を、各々、$p_1$、$p_2$、$p_3$とし、2番目の手番、例えば、情報集合12で、変更(Change)を選ぶ確率を$r_{12}$とする。以上をまとめると、貴方の行動戦略を$(p,r)$と表す。ただし、$p=(p_1,p_2,p_3)$、$p_1+p_2+p_3=1$、$p_1,p_2,p_3\ge 0$、$r=\left( r_{12}, r_{13}, r_{21}, r_{23}, r_{31}, r_{32} \right)$、$0 \le r_{12} \le 1$、$0 \le r_{13} \le 1$、$0 \le r_{21} \le 1$、$0 \le r_{23} \le 1$、$0 \le r_{31} \le 1$、$0 \le r_{32} \le 1$、である。Monty の行動戦略は M と書かれて彼の手番(3個あり)で左の手を取る確率を、各々、$q_1$、$q_2$、$q_3$、とする。すなわち、Monty の行動戦略を$q$で表す。ただし、$q=(q_1,q_2,q_3)$、$0 \le q_1 \le 1$、$0 \le q_2 \le 1$、$0 \le q_3 \le 1$、である。
貴方が行動戦略$(p,r)$をとり、Monty が行動戦略$q$をとった時の、貴方の期待利得(勝つ確率)を$W(p,r,q)$とする。
\[ \begin{align} W(p,r,q) &= \frac{1}{3} p_1 q_1 \left( 1 – r_{12} \right) + \frac{1}{3} p_1 r_{12} \\ &+ \frac{1}{3} p_1 \left( 1 – q_1 \right) \left( 1 – r_{13} \right) + \frac{1}{3} p_1 r_{13} \\ &+ \frac{1}{3} p_2 r_{23} + \frac{1}{3} p_2 \left( 1 – q_2 \right) \left( 1 – r_{23} \right) \\ &+ \frac{1}{3} p_3 r_{32} + \frac{1}{3} p_3 \left( 1 – q_3 \right) \left( 1 – r_{32} \right) \\ &+ \frac{1}{3} p_2 q_2 \left( 1 – r_{21} \right) + \frac{1}{3} p_2 r_{21} \\ &+ \frac{1}{3} p_3 r_{31} + \frac{1}{3} p_3 q_3 \left( 1 – r_{31} \right) \end{align} \]貴方は$p,r$を動かして、$W(p,r,q)$を大きくしようとし、Monty は$q$を動かして、$W(p,r,q)$を小さくしようとする。すなわち、貴方は$\max_{p,r} \min_q W(p,r,q)$を追求し、Monty は$\min_q \max_{p,r} W(p,r,q)$を追求する。
まず、貴方の方から扱う。$p,r$を任意に固定し、$\min_q W(p,r,q)$を求める。$q_1$を含む$W(p,r,q)$の第1項と第3項に関して、
\[ \frac{1}{3} p_1 q_1 \left( 1 – r_{12} \right) + \frac{1}{3} p_1 \left( 1 – q_1 \right) \left( 1 – r_{13} \right) \ge \frac{1}{3} p_1 \min \left\{ 1 – r_{12}, 1 – r_{13} \right\} \]が成り立つ($q_1$は最小値を与える項が左なら$1$、右なら$0$である)。$q_2$を含む第6項と第9項、$q_3$を含む第8項と第12項、も同様に考えると(他の項は$q$に依存しないので)、
\[ \begin{align} \min_q W(p,r,q) &= \frac{1}{3} p_1 \left[ \min \left\{ 1 – r_{12}, 1 – r_{13} \right\} + r_{12} + r_{13} \right] \\ &+ \frac{1}{3} p_2 \left[ \min \left\{ 1 – r_{23}, 1 – r_{21} \right\} + r_{21} + r_{23} \right] \\ &+ \frac{1}{3} p_3 \left[ \min \left\{ 1 – r_{32}, 1 – r_{31} \right\} + r_{31} + r_{32} \right] \end{align} \]となる。この$\min_q W(p,r,q)$を$p,r$を動かして、最大にする。$\min_q W(p,r,q)$の第1項に注目する。
\[ \frac{1}{3} p_1 \left[ \min \left\{ 1 – r_{12}, 1 – r_{13} \right\} + r_{12} + r_{13} \right] = \begin{cases} \frac{1}{3} p_1 \left[ 1 + r_{12} \right] & r_{12} \le r_{13} \\ \frac{1}{3} p_1 \left[ 1 + r_{13} \right] & r_{12} \ge r_{13} \end{cases} \]第1項は、$r_{12}$と$r_{13}$の中で小さいか等しい方がより大きくなれば、大きくなり、第1項以外には$r_{12}$と$r_{13}$がないので、第1項の最大値は$r_{12}=r_{13}=1$の時、$\frac{2}{3} p_1$となる。他の第2項、第3項も同様に考えて、
\[ \max_{p,r} \min_q W(p,r,q) = \frac{2}{3} \left( p_1 + p_2 + p_3 \right) = \frac{2}{3} \]最大値を与えるのは、$p$は任意、$r$は$r_{12}=r_{13}=r_{21}=r_{23}=r_{31}=r_{32}=1$である。
次に、Monty の方から扱う。$q$を任意に固定し、$\max_{p,r} W(p,r,q)$を求める。$W(p,r,q)$の第1項と第2項に注目する。$0 \le \frac{1}{3} p_1 q_1 \le \frac{1}{3} p_1$なので、
\[ \frac{1}{3} p_1 q_1 \left( 1 – r_{12} \right) + \frac{1}{3} p_1 r_{12} \le \frac{1}{3} p_1 \]が成り立つ($r_{12}=1$である)。他も同様に考えると、
\[ \max_{p,r} W(p,r,q) = \frac{1}{3} p_1 + \frac{1}{3} p_1 + \frac{1}{3} p_2 + \frac{1}{3} p_2 + \frac{1}{3} p_3 + \frac{1}{3} p_3 = \frac{2}{3} \left( p_1 + p_2 + p_3 \right) = \frac{2}{3} \]これは$q$を含まないので、$\min_q \max_{p,r} W(p,r,q) = \max_{p,r} W(p,r,q) = \frac{2}{3}$となる。最小値を与える$q$は任意である。
以上で、次のことが証明された。
\[ \begin{align} \max_{p,r} \min_q W(p,r,q) &= \min_q \max_{p,r} W(p,r,q) = \frac{2}{3} \\ \min_q W(p^*,r^*,q) &= \frac{2}{3} \\ \max_{p,r} W(p,r,q^*) &= \frac{2}{3} \\ \end{align} \]ただし、$p^*$は任意、$r^*$は$r^*_{12}=r^*_{13}=r^*_{21}=r^*_{23}=r^*_{31}=r^*_{32}=1$であり、$q^*$は任意である。
言葉で述べると、行動戦略における、貴方の最適戦略(マックスミニ戦略)は$\left( p^*, r^* \right)$であり、Monty の最適戦略(ミニマックス戦略)は$q^*$であり、ゲームの値は$\frac{2}{3}$である。
また、特に、$\max_{p,r} W(p,r,q) = W(p^*,r^*,q) = \frac{2}{3}$となっている。
次に、行動戦略と混合戦略の関係を求める。その前に、純粋戦略を列挙する。純粋戦略とは(貴方または Monty)の各手番でどの手をとるかを決めたものである。貴方の最初の手番を B で表し、2番目の手番(6個ある)をその情報集合12、13、21、23、31、32、で表すことにする。Monty の手番(3個ある)をその情報集合に(左から番号を付けて)M1、M2、M3、で表すことにする。貴方の手番 B では3個の手があり、他の6個の手番では、維持(Keep)または変更(Change)の2個の手があるので、純粋戦略の個数は$3*2^6=192$である。Monty の3個の手番には2個の手があるので、純粋戦略の個数は$2^3=8$である。従って、貴方の混合戦略は各要素が$0$以上で総和が$1$である、$192$次元のベクトルであり、Monty の混合戦略は各要素が$0$以上で総和が$1$である、$8$次元のベクトルである。
純粋戦略の表記を工夫する。$\left( b=i, f_{12} = j_{12}, f_{13} = j_{13}, f_{21} = j_{21}, f_{23} = j_{23}, f_{31} = j_{31}, f_{32} = j_{32} \right)$(括弧の中の順序は入れ替えてもよく、$b$は最初の手番でとる箱を表す変数、$f_{12}$等は手番12でとる行為、維持か変更、を表す変数を意味する)、ただし、$i \in \left\{ 1, 2, 3 \right\}$、$j_{st} \in \left\{ \text{K}, \text{C} \right\} \left( s,t = 1,2,3, s \not= t \right)$であり、貴方が最初の手番で箱$i$を選び、2番目の手番で、例えば、$st$ならば、$j_{st}$をとる(K ならば維持、C ならば変更)純粋戦略を意味する。貴方の混合戦略$x$も純粋戦略$\left( b=i, f_{12} = j_{12}, f_{13} = j_{13}, f_{21} = j_{21}, f_{23} = j_{23}, f_{31} = j_{31}, f_{32} = j_{32} \right)$をとる確率を$x \left( b=i, f_{12} = j_{12}, f_{13} = j_{13}, f_{21} = j_{21}, f_{23} = j_{23}, f_{31} = j_{31}, f_{32} = j_{32} \right)$と表記する。もちろん、$i \in \left\{ 1, 2, 3 \right\}$、$j_{st} \in \left\{ \text{K}, \text{C} \right\} \left( s,t = 1,2,3, s \not= t \right)$に対して、
\[ x \left( b=i, f_{12} = j_{12}, f_{13} = j_{13}, f_{21} = j_{21}, f_{23} = j_{23}, f_{31} = j_{31}, f_{32} = j_{32} \right) \ge 0 \]であり、
\[ \sum_{i \in \left\{ 1, 2, 3 \right\}, j_{st} \in \left\{ \text{K}, \text{C} \right\} \left( s,t = 1,2,3, s \not= t \right)}{ x \left( b=i, f_{12} = j_{12}, f_{13} = j_{13}, f_{21} = j_{21}, f_{23} = j_{23}, f_{31} = j_{31}, f_{32} = j_{32} \right) } = 1 \]である。更に、次のような略記法を利用する。例えば、
\[ x \left( b=i, f_{12} = j_{12} \right) = \sum_{j_{st} \in \left\{ \text{K}, \text{C} \right\} \left( s,t = 1,2,3, (s,t) \not= (1,2), s \not= t \right)}{ x \left( b=i, f_{12} = j_{12}, f_{13} = j_{13}, f_{21} = j_{21}, f_{23} = j_{23}, f_{31} = j_{31}, f_{32} = j_{32} \right) } \]すなわち、$x \left( \cdots \right)$で、その括弧内に書かれていない、$b$、$f_{st} \left( s,t = 1,2,3, s \not= t \right)$に対しては、その部分の総和を行ったもの、を表す。この表記を使えば、$x()=1$である。
Monty の純粋戦略を$\left(m_1=s_1, m_2=s_2, m_3=s_3 \right)$(括弧の中の順序は入れ替えてもよく、$m_i$は Monty の手番 M$i$ で開ける箱を表す変数を意味する)で表す。ただし、$s_1 \in \left\{ 2, 3 \right\}$、$s_2 \in \left\{ 1, 3 \right\}$、$s_3 \in \left\{ 1, 2 \right\}$であり、Monty が手番 M$i$ で$s_i$を選ぶことを意味する。ただし、$i=1,2,3$である。Monty の混合戦略$y$も純粋戦略$\left(m_1=s_1, m_2=s_2, m_3=s_3 \right)$をとる確率を$y \left(m_1=s_1, m_2=s_2, m_3=s_3 \right)$と表記する。もちろん、$s_1 \in \left\{ 2, 3 \right\}$、$s_2 \in \left\{ 1, 3 \right\}$、$s_3 \in \left\{ 1, 2 \right\}$に対して、
\[ y \left(m_1=s_1, m_2=s_2, m_3=s_3 \right) \ge 0 \]であり、
\[ \sum_{s_1 \in \left\{ 2, 3 \right\}, s_2 \in \left\{ 1, 3 \right\}, s_3 \in \left\{ 1, 2 \right\} }{ y \left(m_1=s_1, m_2=s_2, m_3=s_3 \right) } = 1 \]である。
以上の準備の下、貴方の混合戦略$x$が与えられると、それから、行動戦略$(p,r)$が次のように求められる。
\[ \begin{align} p_i &= x \left( b=i \right) &\left( i \in \left\{ 1, 2, 3 \right\} \right) \\ r_{st} &= \frac{x \left( b=s, f_{st}= \text{C} \right)}{x \left( b=s, f_{st}= \text{C} \right) + x \left( b=s, f_{st}= \text{K} \right)} &\left( s,t = 1,2,3, s \not= t \right) \end{align} \]Monty の混合戦略$y$が与えられると、それから、行動戦略$q$が次のように求められる。
\[ q_1 = y \left( m_1 = 2 \right) \\ q_2 = y \left( m_2 = 1 \right) \\ q_3 = y \left( m_3 = 1 \right) \]すなわち、貴方とMonty の混合戦略$x, y$が与えられると、行動戦略$(p,r), q$が求まる。
貴方の混合戦略$x^*$と Monty の混合戦略$y^*$を次のように定義する。
\[ \begin{align} x^* \left( b=i, f_{12} = C, f_{13} = C, f_{21} = C, f_{23} = C, f_{31} = C, f_{32} = C \right) &= p_i \left( i = 1,2,3 \right) \\ y^* \left( m_1 = 2, m_2 = 3, m_3 = 2 \right) &= q_1 \\ y^* \left( m_1 = 3, m_2 = 1, m_3 = 2 \right) &= q_2 \\ y^* \left( m_1 = 3, m_2 = 3, m_3 = 1 \right) &= q_3 \end{align} \]ただし、$p = \left( p_1, p_2, p_3 \right)$は$p_1, p_2, p_3 \ge 0$、$p_1 + p_2 + p_3 = 1$を満たし、$q = \left( q_1, q_2, q_3 \right)$は$0 \le q_1 \le 1$、$0 \le q_2 \le 1$、$0 \le q_3 \le 1$を満たす。また、言及されていない$x^*,y^*$の要素は$0$である。
この時、次が成り立つ。
貴方の混合戦略$x^*$から行動戦略を求めると、行動戦略における貴方の最適戦略$\left( p^*, r^* \right)$が求まる。
また、Monty の混合戦略$y^*$から行動戦略を求めると、行動戦略における Monty の最適戦略$q^*$が求まる。
さて、貴方とMonty の混合戦略$x, y$が与えられた時の貴方の期待利得(勝つ確率)$W \left( x, y \right)$は混合戦略$x, y$から得られる行動戦略$(p,r), q$を利用して次のように求められる。
\[ W \left( x, y \right) = W \left( p, r, q \right) \]以上の事から、$W \left( x^*, y \right) = W \left( p^*, r^*, q \right) = \max_x W \left( x, y \right) = \frac{2}{3}$が成り立つ。これより、$\min_y \max_x W \left( x, y \right) = \frac{2}{3}$と$\max_x \min_y W \left( x, y \right) \ge W \left( x^*, y \right) = \frac{2}{3}$である。また、$\max_x \min_y W \left( x, y \right) \le \min_y \max_x W \left( x, y \right)$が何時も成立するので、結局、次ぎが成り立つ。
\[ \max_x \min_y W \left( x, y \right) = \min_y \max_x W \left( x, y \right) = \frac{2}{3} \\ \min_y W \left( x^*, y \right) = \frac{2}{3} \\ \max_x W \left( x, y^* \right) = \frac{2}{3} \]すなわち、混合戦略における貴方の最適戦略(マックスミニ戦略)は$x^*$であり、Monty の最適戦略(ミニマックス戦略)は$y^*$であり、ゲームの値は$\frac{2}{3}$である。
Monty Hall Problem を体験したい場合は、これを利用して下さい。