最新は1.1版です。
シンプレックス法で線形計画問題(最大化問題)を解くプログラムです。一度に最適解を求めることも、 ステップを追って求めることも可能です。線形計画法やシンプレックス法の基本的なこと等に関しては、「オペレーションズ・リサーチ入門」の該当する部分を参考にして下さい。
線形計画法
複数変数の複数個数の1次不等式制約の下、1次式の目的関数の最大値を求める。
利用方法
データ入力
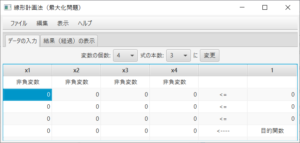
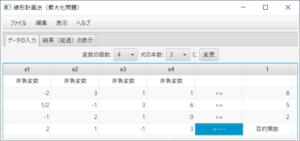
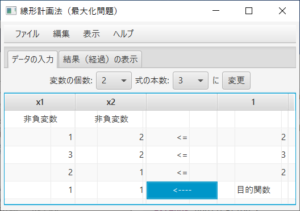
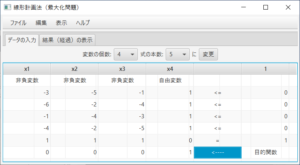
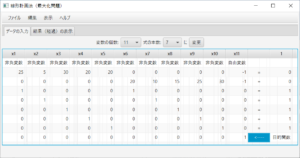
(必要ならば)「データの入力」タブを表示し、(必要ならば)変数の個数、式の本数を変更し「変更」ボタンを押す。このプログラムは最大化問題を解くプログラムなので、最小化問題を解く場合はあらかじめ目的関数を-1倍して最大化問題に変更しておくこと。制約式の係数と定数項を入力する。非負変数でない場合は「非負変数」のセルをクリックし「自由変数」を選ぶ。制約式のタイプとして、「<=」、「=」、「>=」のどれかを選ぶ。目的関数の係数は一番下の行に入力する。入力できる係数は有理数までである。5、10.6、-5/6、2+3/4、等、整数、小数点数、分数(帯分数も可)を入力できる。
結果(経過)の表示
「結果(経過)の表示」タブを表示する。(必要ならば)余裕変数等を自動的に追加して最初のシンプレックス表を求め、この時点での状況(最適解、非有界、等)がステータスバーに表示される。「解く」ボタンを押せば、解が求まる。「ステップ実行」がチェックされていれば、シンプレックス法を1ステップずつ実行する。
例1(実行不可能)
次の線形計画問題(「線形数学」竹内啓著、培風館、p.37より)を解く。
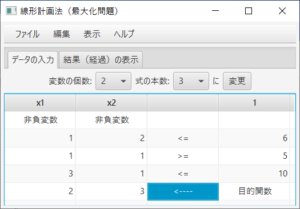
\begin{equation} \max 2x_1 + 3x_2 \\ \textrm{s.t.} \left\{ \begin{array}{c} x_1& + 2x_2& \le 6 \\ x_1& + x_2& \ge 5 \\ 3x_1& + x_2& \le 10 \\ x_1 \ge 0,& x_2 \ge 0& \end{array} \right. \end{equation}(必要ならば)「データの入力」タブを表示して、変数の個数を2個、式の本数を3本に変更し、データを入力する。「結果(経過)の表示」タブを表示すると、
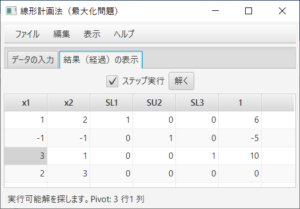
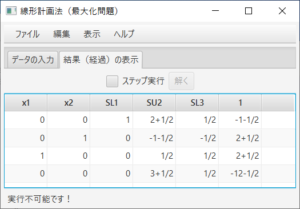
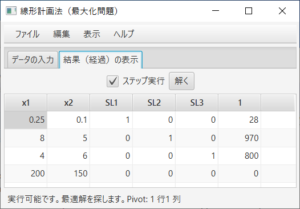
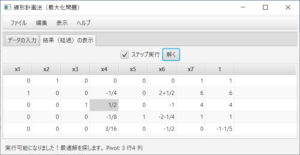
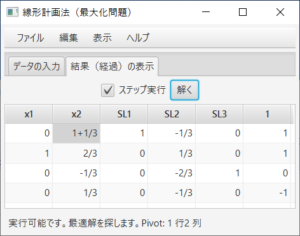
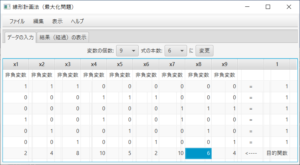
余裕変数(SL)と余剰変数(SU)が追加され、最初のシンプレックス表が表示される。ステータスバーにより、実行可能解を探そうとすること、3行1列がピボットであることが分かる。ここでは、「ステップ実行」のチェックをはずし、答えを求める。「解く」ボタンを押すと、
となり、ステータスバーにより、実行不可能であることが分かる。
例2(非有界)
次の線形計画問題を解く。
\begin{equation} \max 2x_1 + x_2 – x_3 + 3x_4 \\ \textrm{s.t.} \left\{ \begin{array}{c} -2x_1& + 3x_2& + x_3& + x_4& \le 8 \\ \frac{1}{2}x_1& – x_2& + 3x_3& + 6x_4& \le 5 \\ -x_1& + 2x_2& + x_3& & \le 2 \\ x_1 \ge 0,& x_2 \ge 0,& x_3 \ge 0,& x_4 \ge 0& \end{array} \right. \end{equation}(必要ならば)「データの入力」タブを表示して、データを入力する。「結果(経過)の表示」タブを表示すると、
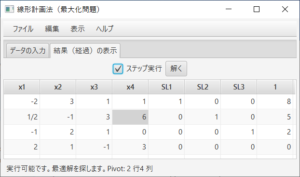
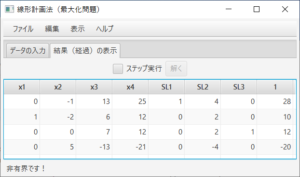
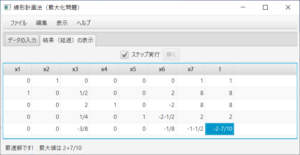
余裕変数が追加され、最初のシンプレックス表が表示される。ステータスバーにより、実行可能であり、最適解を探そうとすること、2行4列がピボットであることがわかる。ここでは、「ステップ実行」のチェックをはずし、答えを求める。「解く」ボタンを押すと、
となり、ステータスバーにより、非有界であることが分かる。
例3(通常)
次の線形計画問題(”Cooperative Game Theory and Applications” by Imma Curiel, p.21より)を解く。
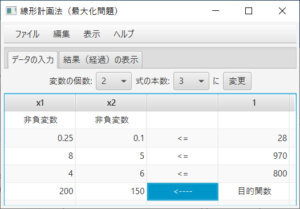
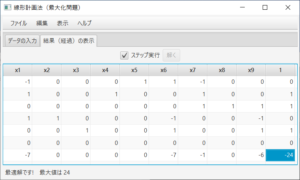
\begin{equation} \max 200x_1 + 150x_2 \\ \textrm{s.t.} \left\{ \begin{array}{c} 0.25x_1& + 0.1x_2& \le 28 \\ 8x_1& + 5x_2& \le 970 \\ 4x_1& + 6x_2& \le 800 \\ x_1 \ge 0,& x_2 \ge 0& \end{array} \right. \end{equation}(必要ならば)「データの入力」タブを表示して、変数の個数を2個、式の本数を3本に変更し、データを入力する。「結果(経過)の表示」タブを表示すると、
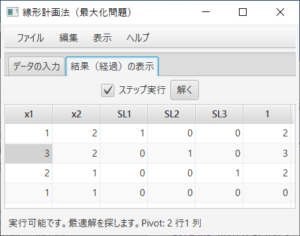
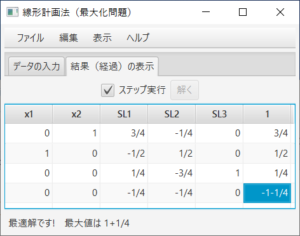
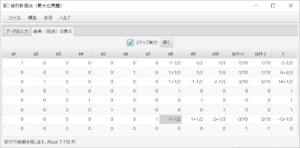
余裕変数が追加され、最初のシンプレックス表が表示される。ステータスバーにより、実行可能であること、最適解を探そうとしていること、1行1列がピボットであることが分かる。ここでは、「ステップ実行」のチェックをはずし、答えを求める。「解く」ボタンを押すと、
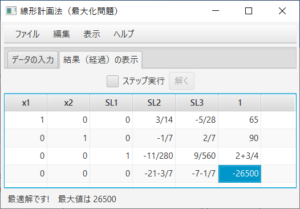
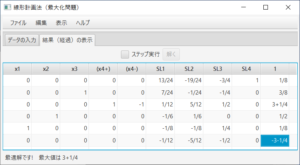
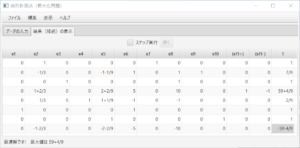
となり、ステータスバーにより、最適解が求まり、最大値は26,500であることが分かる。表を読むことにより、$x_1=65$、$x_2=90$の時、最大値が26,500であり、その時の双対変数(潜在価格)の値が0、21+3/7、7+1/7であることが分かる。
例4(縮退1)
次の線形計画問題(「線型不等式とその応用」長堀長慶著、岩波書店、p.73より)を解く。
\begin{equation} \max 0.2x_1 + \frac{11}{80}x_4 + \frac{6}{5}x_7 \\ \textrm{s.t.} \left\{ \begin{array}{c} & x_2& & & & & + x_7& = 1 \\ 0.4x_1& & + x_3& + 0.4x_4& & & + 6.4x_7& = 6.4 \\ 0.9x_1& & & – 0.35x_4& + x_5& & + 6.4x_7& = 6.4 \\ 0.4x_1& & & – 0.1x_4& & + x_6& + 2.4x_7& = 2.4 \\ x_1 \ge 0,& x_2 \ge 0,& x_3 \ge 0,& x_4 \ge 0,& x_5 \ge 0,& x_6 \ge 0,& x_7 \ge 0& \end{array} \right. \end{equation}(必要ならば)「データの入力」タブを表示して、変数の個数を7個、式の本数を4本に変更し、データを入力する。
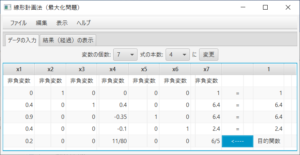
「結果(経過)の表示」タブを表示すると、
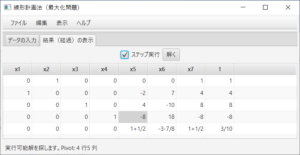
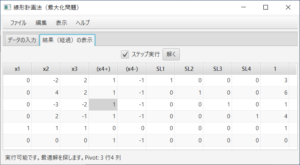
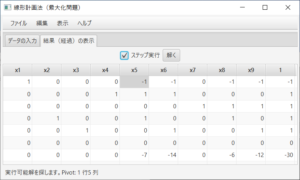
最初のシンプレックス表が表示される。ステータスバーにより、実行可能解を探そうとしていること、4行5列がピボットであることが分かる。ここでは、(必要ならば)「ステップ実行」のチェックし、シンプレックス法を1ステップずつ実行する。「解く」ボタンを必要な回数だけ押す。
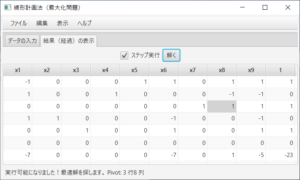
まず、実行可能になり、最適解を探そうとしていること、および、ピボットが3行4列であることが分かり、次に 最適解が求まる。$x_1=8$、$x_2=1$、$x_3=0$、$x_4=8$、$x_5=2$、$x_6=x_7=0$の時、最大値$2.7$である。(上記のシンプレックス表ではピボットの選び方が幸運だったため、最右列がゼロにならなかった。しかし、最初のシンプレックス表で、ピボットを2行7列にすれば、最右列にゼロが現れる。)
例5(縮退2)
次の線形計画問題(「線形数学」竹内啓著、培風館、p.33より)を解く。
\begin{equation} \max x_1 + x_2 \\ \textrm{s.t.} \left\{ \begin{array}{c} x_1& + 2x_2& \le 2 \\ 3x_1& + 2x_2& \le 3 \\ 2x_1& + x_2& \le 2 \\ x_1 \ge 0,& x_2 \ge 0& \end{array} \right. \end{equation}(必要ならば)「データの入力」タブを表示して、変数の個数を2個、式の本数を3本に変更し、データを入力する。「結果(経過)の表示」タブを表示すると、
余裕変数が追加され、最初のシンプレックス表が表示される。ステータスバーにより、実行可能であること、最適解を探そうとしていること、2行1列がピボットであることが分かる(3行1列になる場合もある)。ここでは、(必要ならば)「ステップ実行」のチェックし、シンプレックス法を1ステップずつ実行する。「解く」ボタンを必要な回数だけ押すと、
となり、$x_1=1/2$、$x_2=3/4$の時、最大値$5/4$であること、その時の双対変数(潜在価格)の値が、$1/4$、$1/4$、$0$であることが分かる。
例6(行列ゲーム)
次の行列ゲーム(”Game Theory” by Owen, p54より)を解く。
\[ \left( \begin{array}{c} 3 & 6 & 1 & 4 \\ 5 & 2 & 4 & 2 \\ 1 & 4 & 3 & 5 \end{array} \right) \]これを解くには、次の線形計画問題を解けばよい。
\begin{equation} \max x_4 \\ \textrm{s.t.} \left\{ \begin{array}{c} -3x_1& – 5x_2& – x_3& + x_4& \le 0 \\ -6x_1& – 2x_2& – 4x_3& + x_4& \le 0 \\ -x_1& – 4x_2& – 3x_3& + x_4& \le 0 \\ -4x_1& – 2x_2& – 5x_3& + x_4& \le 0 \\ x_1& + x_2& + x_3& & = 1 \\ x_1 \ge 0,& x_2 \ge 0,& x_3 \ge 0& & \end{array} \right. \end{equation}(必要ならば)変数の個数を4個、式の本数を5本に変更し、上記のデータを入力する。変数$x_4$の「非負変数」をクリックし「自由変数」に変える。「結果(経過)の表示」タブを表示すると、
自由変数$x_4$が2個の非負変数に分離され、余裕変数が追加され、最初のシンプレックス表が表示される。ステータスバーにより、実行可能であり、最適解を探そうとしていること、ピボットが3行4列であることが分かる。ここでは「ステップ実行」のチェックをはずし、解を求める。「解く」ボタンを押すと、
となり、プレイヤー1の最適戦略が(1/8, 1/2, 3/8)であり、ゲームの値が3+1/4であることが分かる。また、プレイヤー2の最適戦略が(1/12, 5/12, 1/2, 0)であることも分かる。
例7(割当問題)
次の割当問題(”Cooperative Game Theory and Applications” by Imma Curiel, p.54より)を解く。
\begin{equation} \max 2x_1 + 4x_2 + 8x_3 + 10x_4 + 5x_5 + 2x_6 + 10x_7 + 6x_8 + 4x_9 \\ \textrm{s.t.} \left\{ \begin{array}{c} x_1& + x_2& + x_3& & & & & & & = 1 \\ & & & x_4& + x_5& + x_6& & & & = 1 \\ & & & & & & x_7& + x_8& + x_9& = 1 \\ x_1& & & + x_4& & & + x_7& & & = 1 \\ & x_2& & & + x_5& & & + x_8& & = 1 \\ & & x_3& & & + x_6& & & + x_9& = 1 \\ x_1 \ge 0,& x_2 \ge 0,& x_3 \ge 0,& x_4 \ge 0,& x_5 \ge 0,& x_6 \ge 0,& x_7 \ge 0,& x_8 \ge 0,& x_9 \ge 0& \end{array} \right. \end{equation}(必要ならば)変数の個数を9個、式の本数を6本に変更し、上記のデータを入力する。
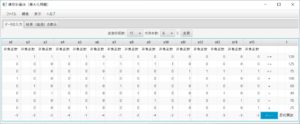
「結果(経過)の表示」タブを表示すると
となり、最初のシンプレックス表が表示される。ステータスバーにより、実行可能解を探そうとしていること、最初のピボットが1行5列であることが分かる。ここでは(必要ならば)「ステップ実行」をチェックして解を求める。「解く」ボタンを必要な回数だけ押す。(下記と異なるピボットが選ばれることもある。)
となり、$x_1=0$、$x_2=0$、$x_3=1$、$x_4=1$、$x_5=0$、$x_6=0$、$x_7=0$、$x_8=1$、$x_9=0$の時、最大値が24であることが分かる。
例8(輸送問題)
次の輸送問題(「問題解決のためのオペレーションズ・リサーチ入門」高井英造、真鍋龍太郎著、日本評論社、第5章より)を解く。
\begin{equation} \max -\left( 3x_1 + 2x_2 + 3x_3 +4x_5 + x_5 +4x_6 + x_7 + 2x_8 + 4x_9 + 2x_{10} + x_{11} + 5x_{13} + 3x_{14} + 2x_{15} \right) \\ \textrm{s.t.} \left\{ \begin{array}{c} x_1& + x_2& + x_3& + x_4& + x_5& & & & & & & & & & & \le 120 \\ & & & & & x_6& + x_7& + x_8& + x_9& + x_{10}& & & & & & \le 125 \\ & & & & & & & & & & x_{11}& + x_{12}& + x_{13}& + x_{14}& + x_{15}& \le 75 \\ x_1& & & & & + x_6& & & & & + x_{11}& & & & & = 100 \\ & x_2& & & & & + x_7& & & & & + x_{12}& & & & = 60 \\ & & x_3& & & & & + x_8& & & & & + x_{13}& & & = 40 \\ & & & x_4& & & & & + x_9& & & & & + x_{14}& & = 75 \\ & & & & x_5& & & & & & + x_{10}& & & & + x_{15}& = 25 \\ x_1 \ge 0,& x_2 \ge 0,& x_3 \ge 0,& x_4 \ge 0,& x_5 \ge 0,& x_6 \ge 0,& x_7 \ge 0,& x_8 \ge 0,& x_9 \ge 0,& x_{10} \ge 0,& x_{11} \ge 0,& x_{12} \ge 0,& x_{13} \ge 0,& x_{14} \ge 0,& x_{15} \ge 0& \end{array} \right. \end{equation}(必要ならば)変数の個数を15個、式の本数を8本に変更し、上記のデータを入力する。
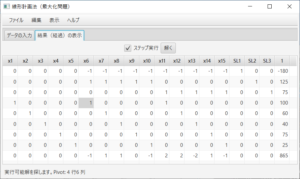
「結果(経過)の表示」タブを表示すると、
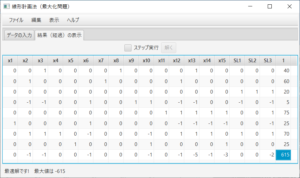
となり、最初のシンプレックス表が表示される。ステータスバーにより、実行可能解を探そうとしていること、最初のピボットが4行6列であることが分かる。ここでは、(必要ならば)「ステップ実行」のチェックを外し、解を求める。「解く」ボタンを押すと、
となり、$x_1=25$、$x_2=x_3=0$、$x_4=70$、$x_5=25$、$x_6=0$、$x_7=60$、$x_8=40$、$x_9=5$、$x_{10}=0$、$x_{11}=75$、$x_{12}=x_{13}=x_{14}=x_{15}=0$の時、最大値が$-615$(最小費用は$615$)であることが分かる。
例9(勝者調整法)
2人のプレイヤーAとBの5品目(可分とする)a、b、c、d、eに対する評価値が次の表のようになっている時、勝者調整法による配分を線形計画法を利用して求める。
| 評価 | a | b | c | d | e | 合計 |
|---|---|---|---|---|---|---|
| A | 25 | 5 | 30 | 20 | 20 | 100 |
| B | 20 | 10 | 15 | 25 | 30 | 100 |
次の線形計画問題を解けばよい。
\begin{equation} \max x_{11} \\ \textrm{s.t.} \left\{ \begin{array}{c} 25x_1& + 5x_2& + 30x_3& + 20x_4& + 20x_5& & & & & & – x_{11}& = 0 \\ & & & & & 20x_6& + 10x_7& + 15x_8& + 25x_9& + 30x_{10}& – x_{11}& = 0 \\ x_1& & & & & + x_6& & & & & & = 1 \\ & x_2& & & & & + x_7& & & & & = 1 \\ & & x_3& & & & & + x_8& & & & = 1 \\ & & & x_4& & & & & + x_9& & & = 1 \\ & & & & x_5& & & & & + x_{10}& & = 1 \\ x_1 \ge 0,& x_2 \ge 0,& x_3 \ge 0,& x_4 \ge 0,& x_5 \ge 0,& x_6 \ge 0,& x_7 \ge 0,& x_8 \ge 0,& x_9 \ge 0,& x_{10} \ge 0& \end{array} \right. \end{equation}(必要ならば)変数の個数を11個、式の本数を7本に変更し、上記のデータを入力する。
「結果(経過)の表示」タブを表示すると
となり、最初のシンプレックス表が表示される。ステータスバーにより、実行可能解を探そうとしていること、最初のピボットが7行8列であることが分かる。ここでは、(必要ならば)「ステップ実行」のチェックを外し、解を求める。「解く」ボタンを押すと、
となり、$x_1=1$、$x_2=0$、$x_3=1$、$x_4=2/9$、$x_5=0$、$x_6=0$、$x_7=1$、$x_8=0$、$x_9=7/9$、$x_{10}=1$の時、最大値が59+4/9であることが分かる。表にすれば次のようになる。プレイヤーAはaとcとdの2/9を貰い、プレイヤーBはbとeとdの7/9を貰う。そのときの利得は59+4/9となる。
| a | b | c | d | e | 合計 | |
|---|---|---|---|---|---|---|
| A | $25$ | $30$ | $\frac{2}{9} \times 20$ | $59 \frac{4}{9}$ | ||
| B | $10$ | $\frac{7}{9} \times 25$ | $30$ | $59 \frac{4}{9}$ |