最新は1.1版です。
種々の投票ルール(多数決ルール、ボルダルール、点数式投票ルール、コープランドルール、シンプソンルール)による勝者(と敗者)を求める。存在すれば、コンドルセ勝者(と敗者)も求める。投票ルールについては「公平のあり方」(大学教育出版)を参考にして下さい。
投票ルール
複数人の候補者に対して、各投票者は望ましい候補者からそうでないない候補者まで選好順位をつけている。(投票者が複数のタイプに分かれ、同じタイプに属する投票者は候補者間に同じ選好順位をつけている。)全ての投票者の選好をまとめて、最も望ましい候補者と最も望ましくない候補者(勝者と敗者と呼ぶ)を選ぶにはどうすれば良いか?
利用方法
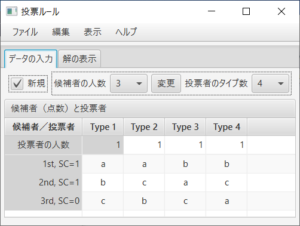
データの入力
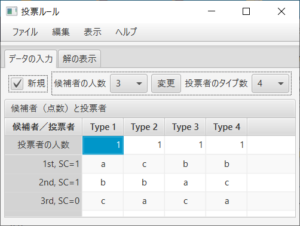
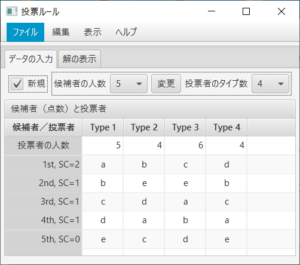
「データの入力」タブでは、まず、(必要ならば)候補者の人数と投票者のタイプ数をコンボボックスを利用して新しい値を指定し、「変更」ボタンを押す。この時、「新規」がチェックされていないならば、変更前の各タイプの人数と候補者間の選好順位をなるべく利用して新しい候補者の人数と投票者のタイプの数が設定される。次に、投票者の各タイプ毎の人数、各タイプ毎の候補者間の選好順、点数式投票ルールの重み(SC)を入力する。
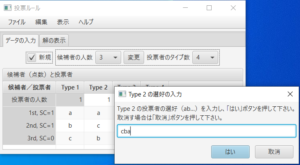
例えば、タイプ2(Type 2)の候補者間の選好順を入力(変更)するには、「type 2」と書いてある部分を左クリックし、現れたダイアログボックスに選好を入力し(ここでは、cbaと入力した)「はい」を押す。
解の表示
「解の表示」タブを押すと、多数決ルール(Plurality)、ボルダルール(Borda)、点数式投票ルール(Scoring voting rule)、コープランドルール(Copeland)、シンプソンルール(Simpson)の解を求めるタブが左側に現れる。存在すれば、コンドルセ(Condorcet)勝者と敗者を求めるタブ、解のまとめを表示するまとめ(Summary)タブ、投票行列と過半数行列を表示する(Vote Matrix)タブもある。
例
次の問題を解く。
候補者の人数はabcdeの5人、投票者のタイプの数は4で、タイプ1の人数は5人、タイプ2の人数は4人、タイプ3の人数は6人、タイプ4の人数は4人である。タイプ1の候補者間の選好順位は1位から5位までa>b>c>d>e、タイプ2はb>e>d>a>c、タイプ3はc>e>a>b>d、タイプ4はd>b>c>a>eである。点数式投票ルールの選好順位が1位から5位までの点数を、2,1,1,1,0とする。
「データの入力」タブで、「候補者の人数」を「5」人にし「変更」ボタンを押す。Type 1から4までの人数を、各々、5,4,6,4と入力する。Type 1から4までの候補者間の選好を「Type ?」と書いてある部分を左クリックし、現れるダイアログボックスに入力し、「リターン」キーを押す。選好順位が1位の点数を2に変更するために、「1st, SC=1」と書いてあるセルをクリックし「2」を入力し「リターン」キーを押す。「解の表示」タブを押すと、左側に「Vote Matrix」、「Plurality」、「Borda」、「Scoring voting rule」、「(s) Condorcet」、「(w) Condorcet」、「Copeland」、「Simpson」、「Summary」の9個のタブがある。「Vote Matirx」タブは投票行列と過半数行列を表示し、「Plurality」タブから「Simpson」タブでは勝者と敗者を求めるためのScoreが表示され、「Summary」タブでは各ルールの勝者と敗者がまとめられている。
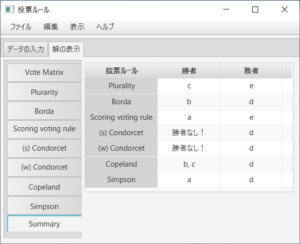
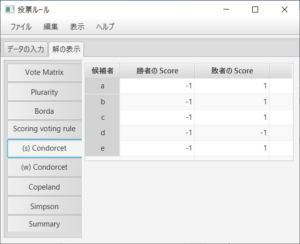
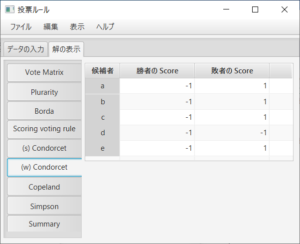
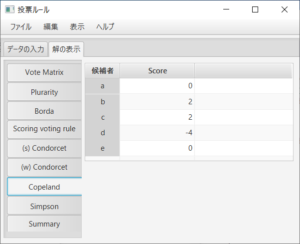
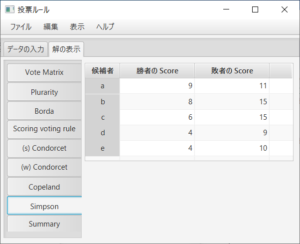
例えば、「Summary」タブを押すと、勝者に関しては、多数決(Plurality)ルールがc、ボルダルールがb、点数が(2,1,1,1,0)の点数式投票ルールがa、(強、弱の)コンドルセ勝者は存在しない、コープランド(Copeland)ルールがbとc、シンプソン(Simpson)ルールがaであることが分かる。敗者に関しては、多数決ルールがe、ボルダルールがd、点数が(2,1,1,1,0)の点数式投票ルールがeである。強コンドルセ敗者が存在しdであるので、弱コンドルセ敗者、コープランド敗者、シンプソン敗者も一致しdとなる。ここで、何も付かないコンドルセ勝者(敗者)は強コンドルセ勝者(敗者)のことである。
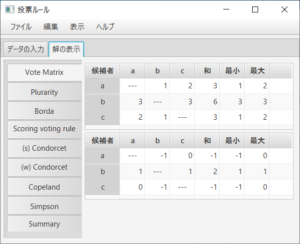
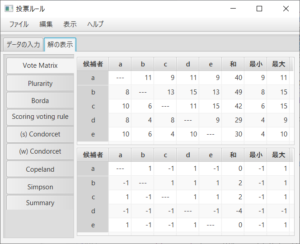
以上の結果を得るために必要なのが次にある投票行列(上の行列)と過半数行列(下の行列)である。
それらの該当する部分を抜き出したのが、「Borda」、「(s) Condorcet」、「(w) Condorcet」、「Coopland」、「Simpson」タブである。
ボルダルールは投票行列の行の「和」の部分、強と弱コンドルセ勝者と敗者は過半数行列の行の「最小」と「最大」の部分であり。
また、コープランドルールは過半数行列の行の「和」の部分、シンプソンルールは投票行列の行の「最小」と「最大」の部分である。
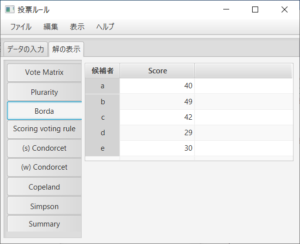
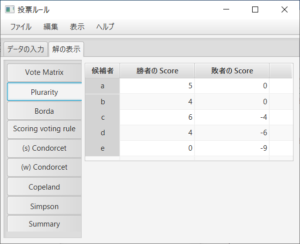
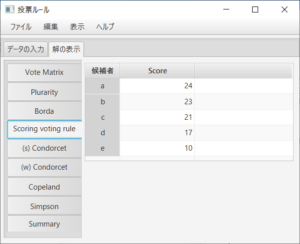
多数決ルールと点数が(2,1,1,1,0)の点数式投票ルールに関しては、定義に基づいて各候補者の点数を計算する必要があり、計算の結果は
のようになる。多数決ルールは点数が(1,0,0,0,0)の点数式投票ルールのことである。