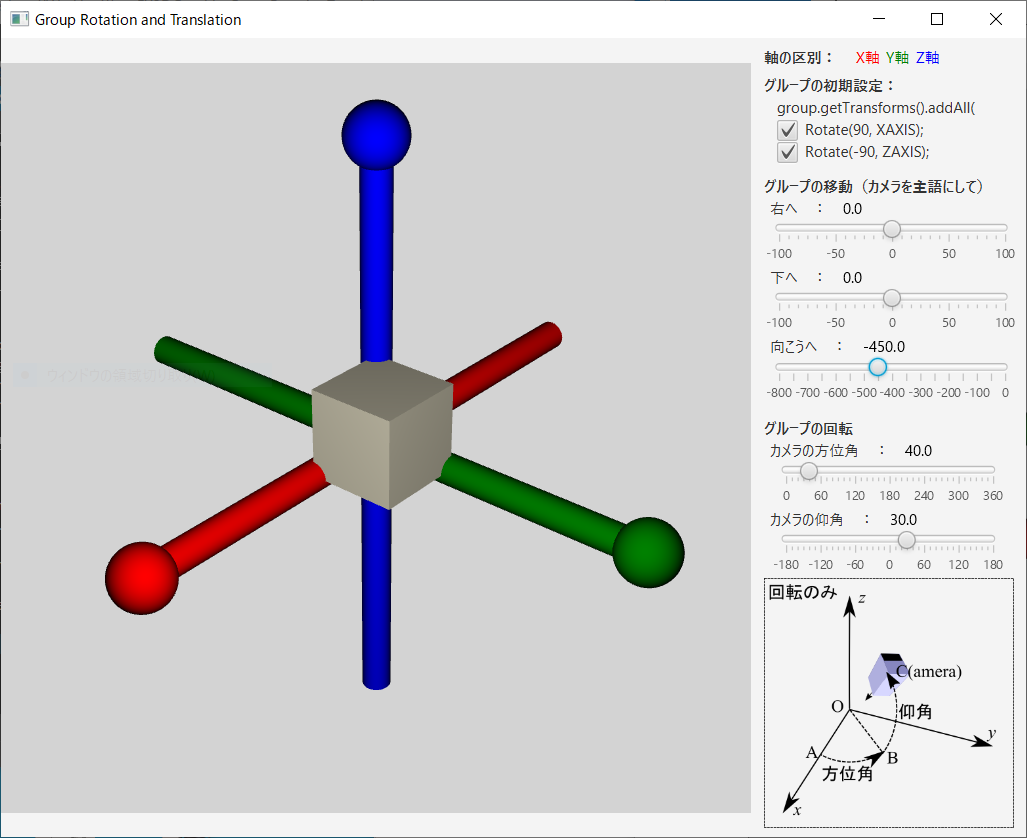
前回(JavaFX 3次元グラフィックス、透視カメラ(PerspectiveCamera)の回転(Rotation)と移動(Translation))はカメラを回転、移動して、固定された被写体(座標軸と立方体)を見る、方法を述べた。今回は、カメラを固定し、被写体を入れたグループを回転、移動して同じことを実現させる。
前回と同様に、PerspectiveCamera(透視カメラ)を引数を true にして作成し、subScene にセットすると、カメラが subScene の中心に向こうを向いて設置され、group の原点が subScene の中心と一致し、X軸が右を向き、Y軸が下を向き、Z軸が向こうを向く。
PerspectiveCamera camera = new PerspectiveCamera(true); Group group = new Group(); SubScene subScene = new SubScene(group, 600, 600, true, SceneAntialiasing.BALANCED); subScene.setCamera(camera);
このままではカメラが原点にあり被写体に近すぎるので、(後で、被写体を入れた group を向こう側へ移動し、)また、ある距離まではカメラで見えて欲しいので、
//camera.setNearClip(0.1); // 既定値0.1で良いので指定しない。 camera.setFarClip(1000); // 既定値は100である。
前回と同様に、group の原点は subScene の中心と一致し、この group に被写体である、座標軸と立方体を、次のように入れる。関数 makeAxes(group) に関しては前回を参照して下さい。
makeAxes(group);
今回の本題の被写体を入れた group の移動と回転に話を進める。現時点では、カメラが subScene の中心に向こうを向いて置かれ、group の原点が subScene の中心と一致し、X軸が右を向き、Y軸が下を向き、Z軸が向こうを向いている。被写体が入っている group を回転させることにより、まず、(数学を勉強した時の標準である)X軸はこちらを、Y軸は右を、Z軸は上を向いているようにし、次に、カメラが方位角と仰角で示される方向から被写体のある原点を眺めるように group を回転し、更に、group を右に、下に、向こう側に移動することである。これを実現する主な部分は
if (isTranslateFirstAgainstLast) {
group.getTransforms().addAll(
/*(0)*/ translate, // 右へ、下へ、向こうへ、によるgroup の移動
/*(1)*/ xAxisRotate, // チェックボックスの真または偽により、原点を通るX軸を回転軸としてgroupを90度、または、0度回転する。
/*(2)*/ zAxisRotate, // チェックボックスの真または偽により、原点を通るZ軸を回転軸としてgroupを-90度、または、0度回転する。
/*(3)*/ azimuthRotate, // 方位角によるgroupの回転
/*(4)*/ elevationRotate // 仰角によるgroupの回転
);
} else {
group.getTransforms().addAll(
/*(1)*/ xAxisRotate, // チェックボックスの真または偽により、原点を通る右向きX軸を回転軸としてgroupを90度、または、0度回転する。
/*(2)*/ zAxisRotate, // チェックボックスの真または偽により、原点を通るZ軸を回転軸としてgroupを-90度、または、0度回転する。
/*(3)*/ azimuthRotate, // 方位角によるgroupの回転
/*(4)*/ elevationRotate, // 仰角によるgroupの回転
/*(5)*/ translate // 右へ、下へ、向こうへ、による group の移動
);
である。if 節と else 節の違いは translate(移動)の位置が最初にあるか最後にあるかである。前回のカメラの回転と移動では translate(移動) は最後にあった。以下で見るように、group の移動の場合、translate が最後にある方が処理が複雑であり、最初にある方が簡単である。回転は group の原点を通る指定された回転軸による回転である。上記において、変数は次のように定義されている。
private Rotate xAxisRotate = new Rotate(0, Rotate.X_AXIS); private Rotate zAxisRotate = new Rotate(0, Rotate.Z_AXIS); private double azimuthRotateAngle = 0; private double elevationRotateAngle = 0; private double right = 0; private double down = 0; private double forward = 0; private Rotate azimuthRotate = new Rotate(azimuthRotateAngle, Rotate.Z_AXIS); private Rotate elevationRotate = new Rotate(elevationRotateAngle, new Point3D(-Math.sin(Math.PI * azimuthRotateAngle/180.0),Math.cos(Math.PI * azimuthRotateAngle/180.0),0)); private Translate translate = new Translate(0, 0, 0);
被写体を入れた group の回転と対比して、カメラ(または、カメラを入れた groupCamera)の回転に関して留意すべきことを再掲する: 各時点での、Rotate.X_AXIS は右向き水平軸、Rotate.Y_AXIS は下向き鉛直軸、Rotate.Z_AXIS は向こう向きの軸、を意味し、その時点でのX軸、Y軸、Z軸ではないことに注意が必要である。また、変換の都度、カメラは自動で、subScene の中心に、向こう側を見るように置き直される、ことにも注意が必要である。
(1)から(5)までをもう少し詳しく説明する。その後、(0)に関して述べる。(1)と(2)は初期に右、下、向こう、を向いている、X軸、Y軸、Z軸を、こちら向き、右向き、上向き、に回転によって変更する部分である。これらの効果を観察可能なように、上図右上にある2個のチェックボックスを設けた。チェックされていない場合は(0度の回転、すなわち、)回転しない。チェックされている場合を説明する。
(1)
チェックボックス「Rotate(90, X_AXIS);」がチェックされたら、
xAxisRotate.setAngle(90);
を実行する。原点を通るX軸を回転軸として group を90度回転する。この結果、X軸は右を向いたまま、Y軸が向こうを向き、Z軸が上を向く。
(2)
チェックボックス「Rotate(-90, Z_AXIS);」がチェックされたら、
zAxisRotate.setAngle(-90);
を実行する。原点を通るZ軸を回転軸として group を-90度回転する。(1)の結果Z軸は上を向いていたので、この結果、X軸はこちらを向き、Y軸は右を向き、Z軸は上を向いた。
次に、方位角と仰角の回転に移る。(下図では方位角と仰角が何かを理解しやすいように、group は既に、(5)で説明する向こう側に移動している。)
(3)
方位角を表すスライダーが更新され、その値を azimuthRotateAngle とする時、原点を通るZ軸を回転軸として、group を -azimuthRotateAngle だけ回転させればよい。既に、変数 azimuthRotate の回転軸としてZ軸(Rotate.Z_AXIS)を設定しているので、
azimuthRotate.setAngle(-azimuthRotateAngle);
を実行すればよい。
(4)
仰角を表すスライダーが更新され、その値を elevationRotateAngle とする時、原点を通る右向き水平軸を回転軸として、group を elevationRotateAngle だけ回転させればよい。この右向き水平軸は group の(現時点での)X軸ではない、ことに注意する。次の1行目で、変数 elevationRotate の回転軸としてこの右向き水平軸を設定している(詳しい「elevationRotate の回転軸の導出」は後述する)。
elevationRotate.setAxis(new Point3D(-Math.sin(Math.PI * azimuthRotateAngle/180.0), Math.cos(Math.PI * azimuthRotateAngle/180.0), 0)); elevationRotate.setAngle(elevationRotateAngle);
を実行すればよい。
(5)
最後に、group を移動することにより、カメラが右へ、下へ、向こうへ移動したように見えることに移る。(別々に処理してもよいが一緒に処理することにした。)これら3つのスライダーが更新され、それぞれの値を right、down、forward とする。これらの値を測る水平軸、垂直軸、向こう向きの軸は group の現時点での)X軸、Y軸、Z軸ではないことに注意する。right、down、forward に対応する group のX座標、Y座標、Z座標の変位 x、y、z は
x = right * Math.sin(Math.PI * azimuthRotateAngle / 180.0) - down * Math.cos(Math.PI * azimuthRotateAngle / 180.0) * Math.sin(Math.PI * elevationRotateAngle / 180.0) + forward * Math.cos(Math.PI * azimuthRotateAngle / 180.0) * Math.cos(Math.PI * elevationRotateAngle / 180.0); y = -right * Math.cos(Math.PI * azimuthRotateAngle / 180.0) - down * Math.sin(Math.PI * azimuthRotateAngle / 180.0) * Math.sin(Math.PI * elevationRotateAngle / 180.0) + forward * Math.sin(Math.PI * azimuthRotateAngle / 180.0) * Math.cos(Math.PI * elevationRotateAngle / 180.0); z = down * Math.cos(Math.PI * elevationRotateAngle / 180.0) + forward * Math.sin(Math.PI * elevationRotateAngle / 180.0);
で与えられるので(詳しい「group 座標における変位の導出」は後述する)、
translate.setX(x); translate.setY(y); translate.setZ(z);
とすればよい。
以上、前回はカメラ(または、カメラを入れた groupCamera)の移動と回転、今回は被写体を入れた group の移動と回転を述べたが、これらの注意事項をまとめる。
カメラ(または、カメラを入れたgroupCamera)の回転に関して:
各時点での、Rotate.X_AXISは右向き水平軸、Rotate.Y_AXISは下向き鉛直軸、Rotate.Z_AXISは向こう向きの軸、を意味し、その時点でのX軸、Y軸、Z軸ではないことに注意が必要である。また、変換の都度、カメラは自動で、subSceneの中心に、向こう側を見るように置き直される、ことにも注意が必要である。
被写体を入れたgroupの移動と回転に関して:
各時点での、原点、Rotate.X_AXIS、Rotate.Y_AXIS、Rotate.Z_AXISはその時点でのgroup の実際の原点、X軸、Y軸、Z軸を意味する。
(0)
(5)において、right、down、forward から x、y、z を求める部分は複雑である。しかし、translate を最初におくと、right、down、forward を測る軸が、group のその時点でのX軸、Y軸、Z軸と一致するので(符号は反対である)、
translate.setX(-right); translate.setY(-down); translate.setZ(-forward);
とすればよい。この後、(1)から(4)を適用しても、上述した被写体を入れた group に関する注意事項から、(1)から(5)を適用した時と同じ結果が得られる。
次に、右側に配置された、スライダー群、等を入れた VBox を含む部分に関して概要を述べる。コードは、前回と同様に、次の通りである。
VBox controlVBox = new VBox(); makeControlVBox(controlVBox); HBox hBox = new HBox(); hBox.setAlignment(Pos.CENTER); hBox.getChildren().addAll(subScene, controlVBox); Scene scene = new Scene(hBox);
スライダー群を含む controlVBox を作成し(makeControlVBox(controlVBox)、この関数の内容も前回と今回で若干異なる。)、subScene とこの controlVBox を入れた hBox を作成し、それを scene に入れる。現時点での、この部分に関する注意事項として、本来ならこの複雑な構造を持つ controlVBox を含む hBox を SceneBuilder で作成したいのだが、SceneBuilder で作成し、実行しても(理由は不明であるが、)正常に作動しなかった。以下では、右へと方位角と仰角のスライダーの処理の部分のみを説明する。
controlVBox における、現在の方位角と仰角の値を表示する Text とそれらを設定する Slider を次のように定義する。(各スライダーの最小値、最大値、初期値、等は makeControlVBox(controlVBox) で設定している。)
private Text textTranslateToRight = new Text("0.0");
private Text textAzimuth = new Text("0.0");
private Text textElevation = new Text("0.0");
private Slider sliderTranslateToRight = new Slider();
private Slider sliderAzimuth = new Slider();
private Slider sliderElevation = new Slider();
スライダー群の処理を記述する、次の関数 handleSliders() を start(Stage) 関数で実行する。
private void handleSliders() {
sliderTranslateToRight.valueProperty().addListener(new ChangeListener<Number>() {
@Override
public void changed(ObservableValue<? extends Number> ov, Number old_val, Number new_val) {
right = (double)new_val;
setTranslates();
}
});
// 他のスライダーの処理は省略する。
sliderAzimuth.valueProperty().addListener(new ChangeListener<Number>() {
@Override
public void changed(ObservableValue<? extends Number> ov, Number old_val, Number new_val) {
if (new_val != null) {
azimuthRotateAngle = (double)new_val;
setAzimuthElevationRotate(); // ここが異なる。前回はsetAzimuthRotate()であった。
}
}
});
sliderElevation.valueProperty().addListener((ObservableValue<? extends Number> ov, Number old_val, Number new_val) -> {
if (new_val != null) {
elevationRotateAngle = (double)new_val;
setAzimuthElevationRotate(); // ここが異なる。前回はsetElevationRotate()であった。
}
});
}
ここで、sliderAzimuth の方は旧来の匿名クラス、sliderElevation の方はラムダ式、を利用して Listener を記述している。また、set*** は
private void setTranslates() { // right、down、forwardを別々に扱わず、一緒に扱った。
double x = -right;
double y = -down;
double z = -forward;
if (!isTranslateFirstAgainstLast) { // rewrite x, y, and z
x = right * Math.sin(Math.PI * azimuthRotateAngle / 180.0) - down * Math.cos(Math.PI * azimuthRotateAngle / 180.0) * Math.sin(Math.PI * elevationRotateAngle / 180.0) + forward * Math.cos(Math.PI * azimuthRotateAngle / 180.0) * Math.cos(Math.PI * elevationRotateAngle / 180.0);
y = -right * Math.cos(Math.PI * azimuthRotateAngle / 180.0) - down * Math.sin(Math.PI * azimuthRotateAngle / 180.0) * Math.sin(Math.PI * elevationRotateAngle / 180.0) + forward * Math.sin(Math.PI * azimuthRotateAngle / 180.0) * Math.cos(Math.PI * elevationRotateAngle / 180.0);
z = down * Math.cos(Math.PI * elevationRotateAngle / 180.0) + forward * Math.sin(Math.PI * elevationRotateAngle / 180.0);
}
translate.setX(x);
translate.setY(y);
translate.setZ(z);
textTranslateToRight.setText(""+right);
textTranslateToDown.setText(""+down);
textTranslateToForward.setText(""+forward);
}
private void setAzimuthElevationRotate( ) {
azimuthRotate.setAngle(-azimuthRotateAngle);
elevationRotate.setAxis(new Point3D(-Math.sin(Math.PI * azimuthRotateAngle / 180.0), Math.cos(Math.PI * azimuthRotateAngle / 180.0), 0));
elevationRotate.setAngle(elevationRotateAngle);
textAzimuth.setText(""+azimuthRotateAngle);
textElevation.setText(""+elevationRotateAngle);
if (!isTranslateFirstAgainstLast) setTranslates();
}
である。前回では、別に扱っていた setAzimuthRotate() と setElevationRotate() を、1つの setAzimuthElevationRotate() にまとめた理由は、elevationRotate.setAxis() の引数に azimuthRotateAngle を含むためである。また、translate を最後に処理する場合(!isTranslateFirstAgainstLast が真の場合)、その処理にその時点での azimuthRotateAngle と elevationRotateAngle を含むためである。
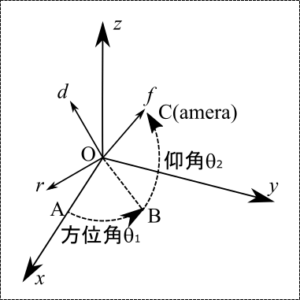
elevationRotateの回転軸の導出
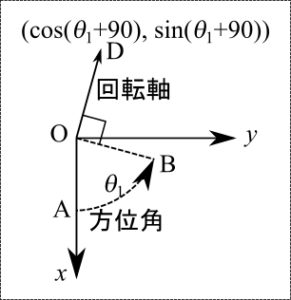
$\theta_1 =$ azimuthRotateAngle、$\theta_2 = $ elevationRotateAngle とする。上図のように、$\theta_1$は平面OAB上にある。$\theta_2$は平面OBC上にある。$\theta_2$だけ回転させる回転軸は平面OAB上にあり、Oを通りOBと直交し、x軸の負の方、y軸の正の方を向いている。この回転軸上の点DをOD=1となるようにとると(下図参照;平面OAB、すなわち、xy平面を描いている。)、Dの座標は $\left( \cos \left(\theta_1 + 90 \right), \sin \left( \theta_1 + 90 \right) \right) = \left( – \sin \theta_1, \cos \theta_1 \right)$
従って、回転軸は$\left( – \sin \theta_1, \cos \theta_1, 0 \right)$である。引数で角度を指定する場合はラジアンで指定することになっており、180度=$\pi$ラジアンなので、Math.PI / 180.0 をかけておく。
group座標における変位の導出
$\theta_1 = $ azimuthRotateAngle、$\theta_2 = $ elevationRotateAngle とする。スライダーの、右への値が $r$、下への値が$d$、向こうへの値が$f$の時、被写体が入っているgroupを左へ$r$、上へ$d$、こちらへ$f$ だけ移動させる必要がある。原点を通り、左へ、上へ、こちらへ、に対応するように、r軸、d軸、f軸をとる(上図参照)。
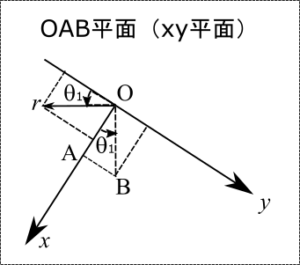
r軸は平面OAB(xy平面)上にあり、d軸とf軸はOBC平面(z軸も含む)上にある。r、d、f軸で測った点$(r, d, f)$をx、y、z軸で測る。r、d、f軸方向の単位ベクトル(長さが1のベクトル)を、各々、$\vec{e_r}$、$\vec{e_d}$、$\vec{e_f}$とし、x、y、z軸方向の単位ベクトルを、各々、$\vec{e_x}$、$\vec{e_y}$、$\vec{e_z}$とする。その時、$r \vec{e_r} + d \vec{e_d} + f \vec{e_f} = x \vec{e_x} + y \vec{e_y} + z \vec{e_z}$となる、$x$、$y$、$z$を求める。OB方向の単位ベクトルを$\vec{e_B}$とする。まず、$\vec{e_r}$、$\vec{e_d}$、$\vec{e_f}$を$\vec{e_x}$、$\vec{e_y}$、$\vec{e_z}$で表す。OAB平面(xy平面)を描くと(下図参照)、
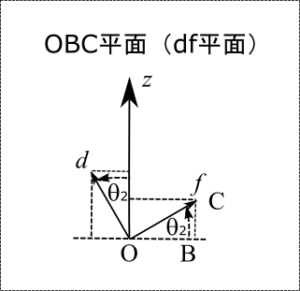
\[ \vec{e_r} = \sin \theta_1 \vec{e_x} – \cos \theta_1 \vec{e_y} \\ \vec{e_B} = \cos \theta_1 \vec{e_x} + \sin \theta_1 \vec{e_y} \]また、OBC平面(df平面)を描くと(下図参照)、
\begin{eqnarray} \vec{e_d} &=& – \sin \theta_2 \vec{e_B} + \cos \theta_2 \vec{e_z} \\ &=& – \cos \theta_1 \sin \theta_2 \vec{e_x} – \sin \theta_1 \sin \theta_2 \vec{e_y} + \cos \theta_2 \vec{e_z} \\ \vec{e_f} &=& \cos \theta_2 \vec{e_B} + \sin \theta_2 \vec{e_z} \\ &=& \cos \theta_1 \cos \theta_2 \vec{e_x} + \sin \theta_1 \cos \theta_2 \vec{e_y} + \sin \theta_2 \vec{e_z} \end{eqnarray}従って、
\begin{eqnarray} r \vec{e_r} + d \vec{e_d} + f \vec{e_f} = &\left( r \sin \theta_1 – d \cos \theta_1 \sin \theta_2 + f \cos \theta_1 \cos \theta_2 \right) \vec{e_x} \\ + &\left( -r \cos \theta_1 – d \sin \theta_1 \sin \theta_2 + f \sin \theta_1 \cos \theta_2 \right) \vec{e_y} \\ + &\left( d \cos \theta_2 + f \sin \theta_2 \right) \vec{e_z} \end{eqnarray}まとめると、
\begin{eqnarray} x &=& &r& \sin \theta_1 – &d& \cos \theta_1 \sin \theta_2 &+& f \cos \theta_1 \cos \theta_2 \\ y &=& -&r& \cos \theta_1 – &d& \sin \theta_1 \sin \theta_2 &+& f \sin \theta_1 \cos \theta_2 \\ z &=& & & &d& \cos \theta_2 &+& f \sin \theta_2 \end{eqnarray}引数で角度を指定する場合はラジアンで指定することになっており、180度=$\pi$ラジアンなので、Math.PI / 180.0 をかけておく。