(正比例に近い)整数による配分の種々の解(ハミルトン法、アダムズ法、ディーン法、ヒル法、ウェブスター法、ジェファーソン法)を(優先法または除数法として)求める。整数による配分とそれぞれの解については、私の講義(「意思決定論」)を参考にして下さい。
データ入力
データの「入力」タブでは、まず、(必要ならば)プレイヤーの人数をコンボボックスを利用して変更する。次に、配分すべき資源の個数\(A\)、各プレイヤーの要求量\(d\)を正の整数で入力する。
解の計算
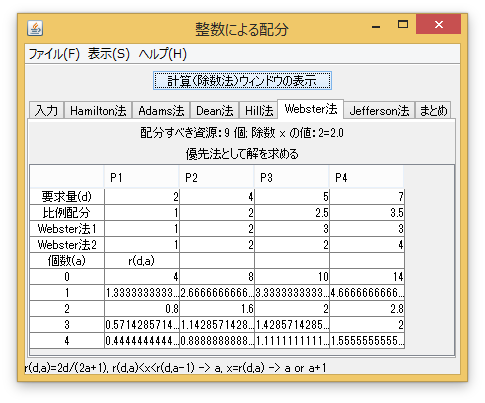
「Hamilton法」から「Jefferson法」タブでは(「Adams法」から「Jefferson法」では優先法として)解を求めている。複数の解がある場合も、それら全てを求めている。
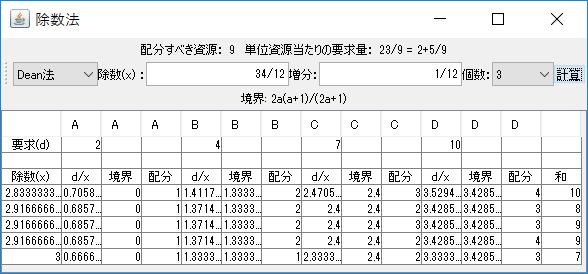
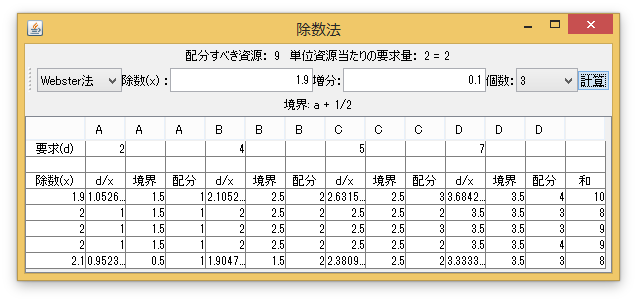
「計算(除数法)ウィンドウの表示」ボタンを押すと、Adams法からJefferson法の解を除数法として求めるためのウィンドウが表示される。求める方法、除数(\(x\))(の初期値)、増分、個数を設定して、「計算」ボタンを押すことで、除数として、初期値から始め、増分を増やして、個数分だけ変化させた時の各配分が計算される。ただし、Hill法の場合は除数の2乗を設定する。増分も除数の2乗の増分である。「和」の列の値が配分すべき資源の個数に一致すれば、その行の配分が求める解である。
例1
次の問題を解く。
\(A\)=10、\(d\)=(19,17,7,5)。
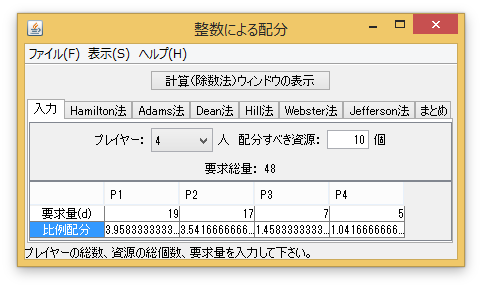
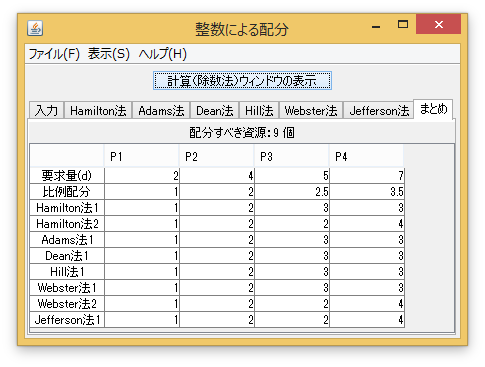
「入力」タブで、「配分すべき資源」を「10」個にし、各プレイヤーの要求量を入力する。例えば、「まとめ」タブを押すと、全ての解が表示される。
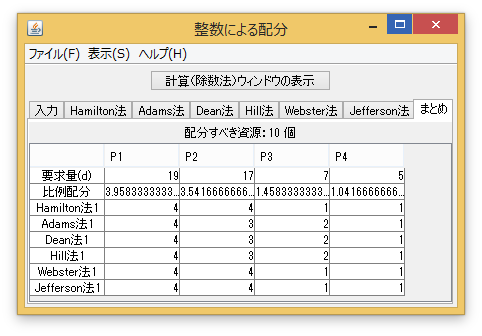
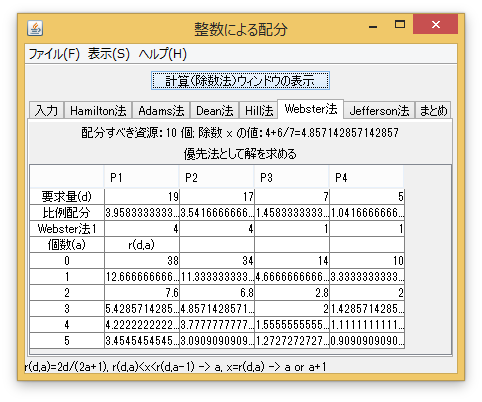
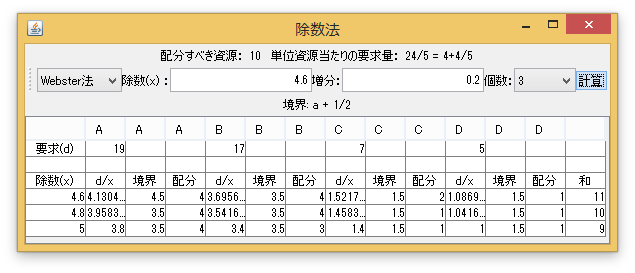
例2
次の問題を解く。
\(A\)=9、\(d\)=(2,4,5,7)。
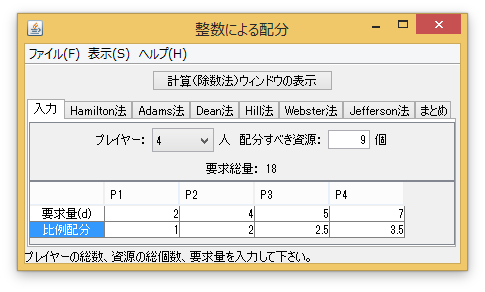
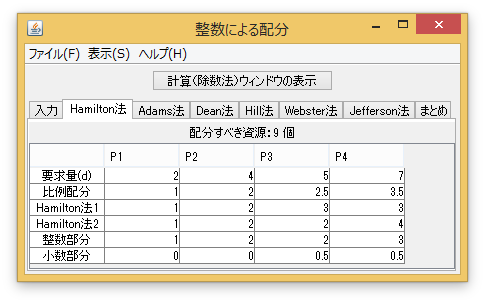
「入力」タブで、「配分すべき資源」を「9」個にし、各プレイヤーの要求量を入力する。例えば、「Hamilton法」タブを押すと、その解が表示される。
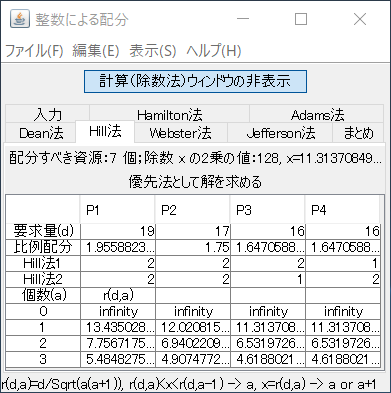
例3(Hill法)
次の問題を解く。
\(A\)=7、\(d\)=(19,17,16,16)。
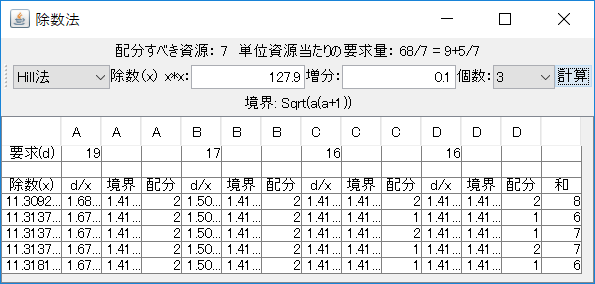
「入力」タブで、「配分すべき資源」を「7」個にし、各プレイヤーの要求量を入力する。「Hill法」タブを押すと、その解が表示される。2通りの解があり、Hill法1とHill法2と示されていることが分かる。これらを除数法を利用して求める。まず、「Hill法」タブの「優先法として解を求める」の右上に表示されている除数\(x\)の2乗の値を記憶する。(どれくらい詳しく記憶するかは、問題によって変わるが、ここでは128と記憶しておく。)「計算(除数法)ウィンドウの表示」ボタンを押すと、「除数法」ウィンドウが表示される、左上のコンボボックスから「Hill法」を選び、除数の2乗の初期値、増分、個数を、「127.9」、「0.1」、「3」と設定し、「計算」ボタンを押す。
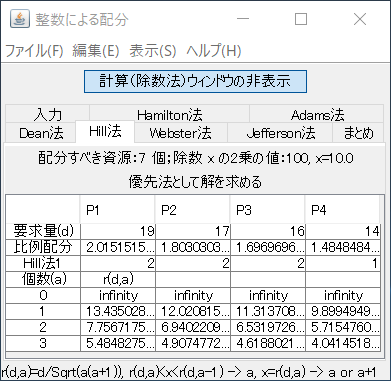
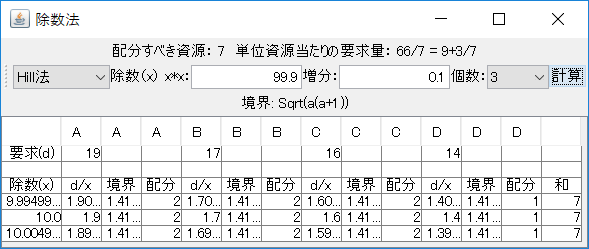
複数個の解を持たない、次の問題を解く。
\(A\)=7、\(d\)=(19,17,16,14)。
優先法と除数法による解法は次の通りである。ここでは、除数の2乗の初期値、増分、個数を、「99.9」、「0.1」、「3」と設定した。
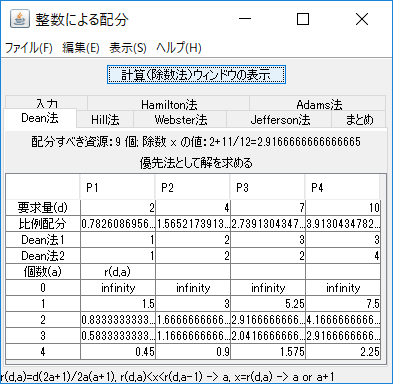
例4(Dean法)
Dean法に複数の解がある、次の問題を解く。
\(A\)=9、\(d\)=(2,4,7,10)。
結果だけを記す。解は、(1,2,3,3)と(1,2,2,4)の2つである。35/12以外の除数では除数法により解が求まらない。