行列の演算 | アプリケーションの利用法

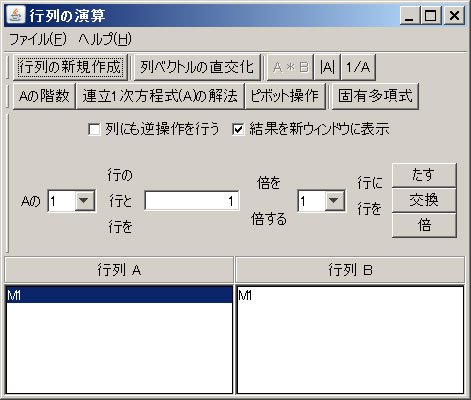
列ベクトルを直交化し、行列の積、行列の階数、逆行列、行列式、固有多項式、固有値を求め、連立1次方程式を解く。線形代数の基本的なこと、及び、ここで利用されている計算方法に関しては、私の講義（「計画数学I」）、または、Shop「風聴き鳥」で販売されている電子書籍（EBook）「線形代数入門」を参考にして下さい。

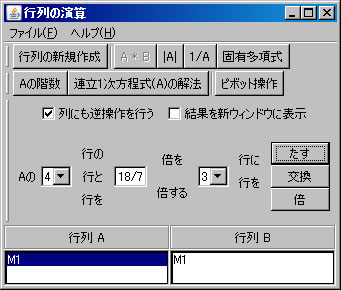
行列の新規作成

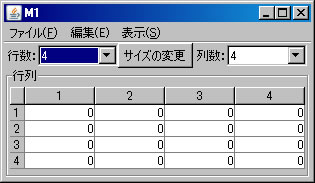
「行列の新規作成」ボタンを押すと、4行4列の正方行列が新しいウィンドウに作成される。名前はタイトルバーに自動的に付けられる。行数と列数を変更し、「サイズの変更」ボタンを押せば、サイズを変更できる。行列の各要素には有理数を入力できる。「-10」、「2/3」、「14.52」等の整数、分数（帯分数ではなく仮分数）、小数が入力できる。しかし、「5+2」のように式を入力して計算結果の「7」を入力することは出来ない。既定では入力した結果が分数表示されるが、「表示」メニューから、他の「小数表示」、「帯分数表示」を選ぶことにより変更できる。また、既定では各セルの幅を自動的に揃えてウィンドウ一杯に表示するが、「表示」メニューの「セルを揃える」のチェックを外すことにより、自動的に揃えないように出来る。

列ベクトルの直交化

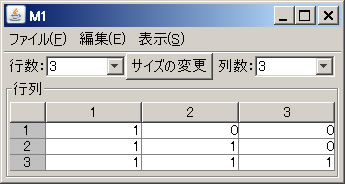
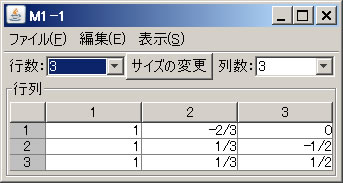
例として、3つの列ベクトル $\left( \begin{array}{r} 1 \\ 1 \\ 1 \end{array} \right), \left( \begin{array}{r} 0 \\ 1 \\ 1 \end{array} \right), \left( \begin{array}{r} 0 \\ 0 \\ 1 \end{array} \right)$ をグラム・シュミットの直交化法により直交化する。必要ならば「行列の新規作成」ボタンを押し、この3個の列ベクトルからなる行列（この例の場合は3行3列の行列）を作成する（ここでは、M1という名前が自動的に付けられている）。

「行列の演算」メインウィンドウに戻り、

「行列A」のりストボックスでM1を選択し、「列ベクトルの直交化」ボタンを押すと、結果が新しいウィンドウM1-1に表示され

直交化されたベクトルは $\left( \begin{array}{r} 1 \\ 1 \\ 1 \end{array} \right), \left( \begin{array}{r} – \frac{2}{3} \\ \frac{1}{3} \\ \frac{1}{3} \end{array} \right), \left( \begin{array}{r} 0 \\ – \frac{1}{2} \\ \frac{1}{2} \end{array} \right)$ となる。

行列の積

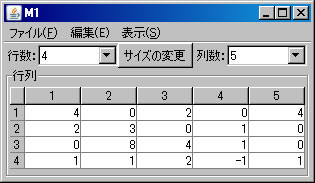
例として、積 $\left( \begin{array}{ccccc} 4 & 0 & 2 & 0 & 4 \\ 2 & 3 & 0 & 1 & 0 \\ 0 & 8 & 4 & 1 & 0 \\ 1 & 1 & 2 & -1 & 1 \end{array} \right) \left( \begin{array}{ccc} 1 & 0 & 1 \\ 6 & 0 & 1 \\ 1 & 3 & 0 \\ -2 & 2 & -4 \\ 1 & -5 & 2 \end{array} \right)$ の例を計算する。必要ならば「行列の新規作成」ボタンを2回押し、この2つの行列を作成する（ここでは、M1とM2という名前が自動的に付けられている）。

「行列の演算」メインウィンドウに戻り、

「行列A」のリストボックスでM1を選択し、「行列B」のリストボックスでM2を選択し、「A*B」ボタンを押す。結果が新しいウィンドウ(M1)*(M2)に表示される。

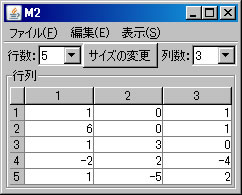
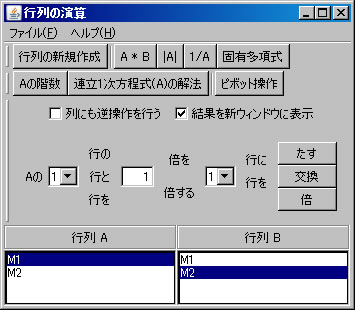
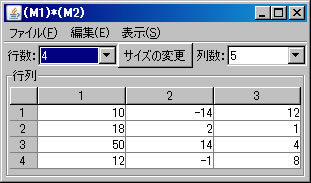
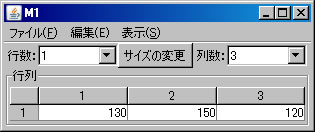
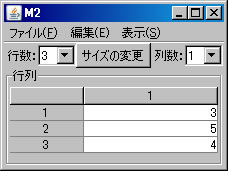
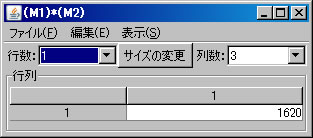
他の行列の積の例として、 $\left( \begin{array}{rrr} 130 & 150 & 120 \end{array} \right) \left( \begin{array}{r} 3 \\ 5 \\ 4 \end{array} \right)$ を求める。左の行ベクトルを列ベクトルと見なすと、ベクトルの内積でもある。

「行列の演算」メインウィンドウに戻り、

階数

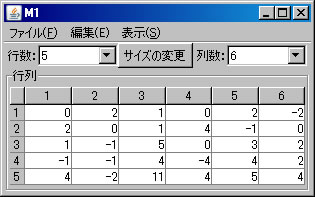
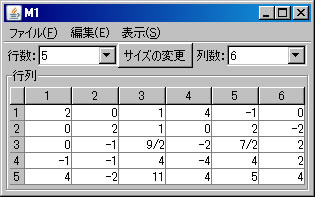
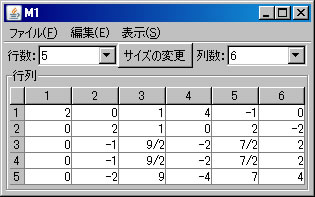
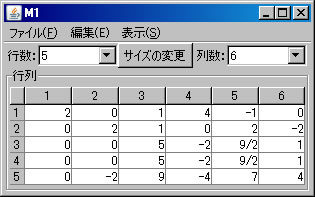
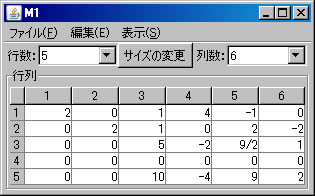
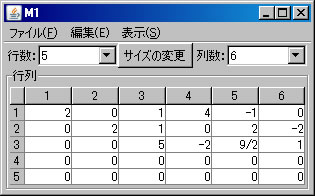
例として $\left( \begin{array}{rrrrrr} 0 & 2 & 1 & 0 & 2 & -2 \\ 2 & 0 & 1 & 4 & -1 & 0 \\ 1 & -1 & 5 & 0 & 3 & 2 \\ -1 & -1 & 4 & -4 & 4 & 2 \\ 4 & -2 & 11 & 4 & 5 & 4 \end{array} \right)$ の階数を求める。必要ならば、「行列の新規作成」ボタンを押し、サイズを5行6列に変更し、この行列を作成する。（ここではM1という名前がついている。）「行列の演算」ウィンドウに戻り、

「行列A」リストボックスでM1を選択し、「Aの階数」ボタンを押す。「M1の階数」ウィンドウのステータスバーに答えが表示される。

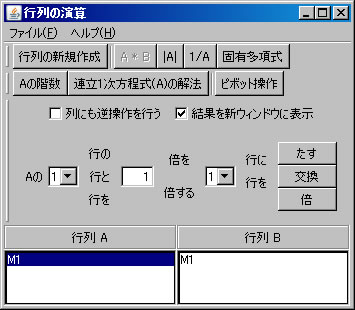
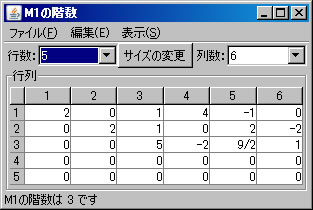
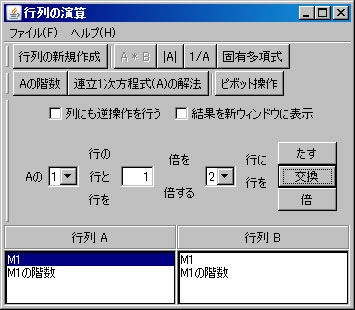
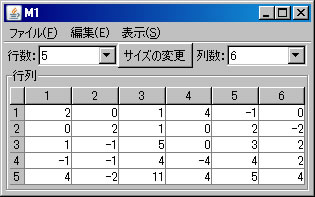
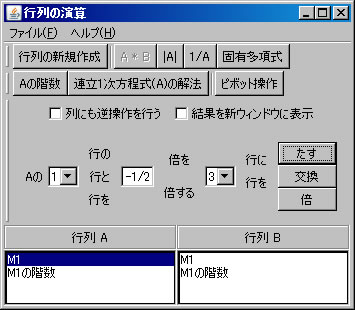
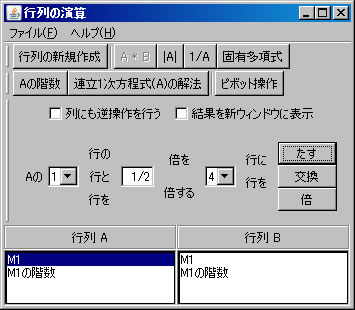
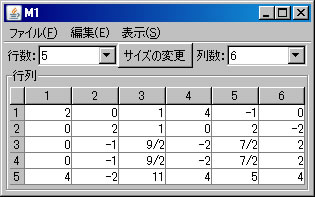
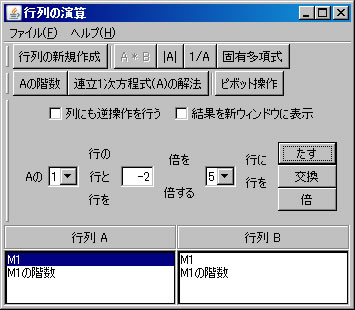
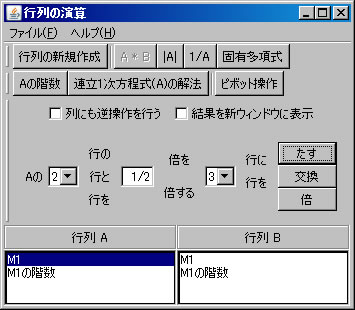
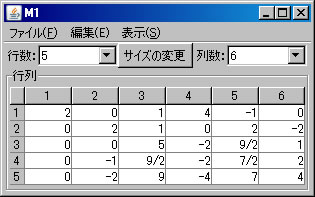
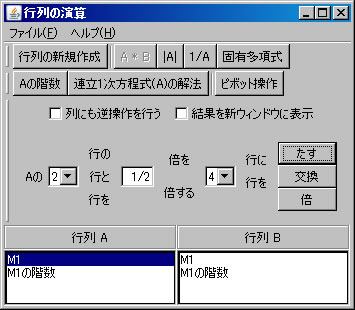
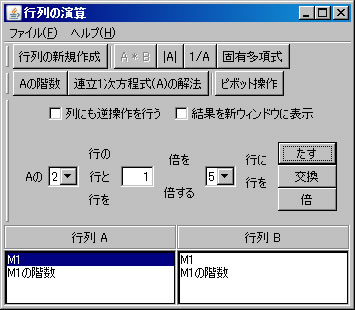
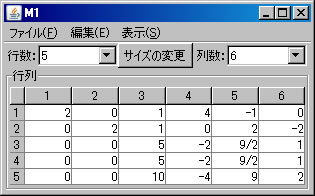
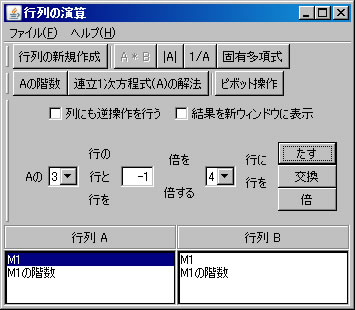
行列の階数を「Aの階数」ボタンを1回押すだけで求めたが、今度は、行列の基本変形を利用して求める。「行列の演算」ウィンドウでM1を選択する。（解く経過を残さない場合は、「結果を新ウィンドウに表示」のチェックを外す。）1行と2行を交換する。

1行の-1/2倍を3行にたす

1行の1/2倍を4行にたす

1行の-2倍を5行にたす

2行の1/2倍を3行にたす

2行の1/2倍を4行にたす

2行の1倍を5行にたす

3行の-1倍を4行にたし、-2倍を5行にたす

となり、階数が3であることが分かる。

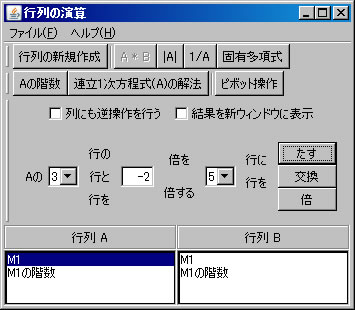
同次連立1次方程式

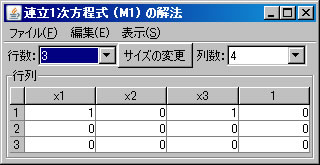
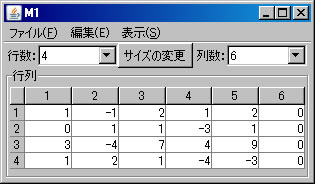
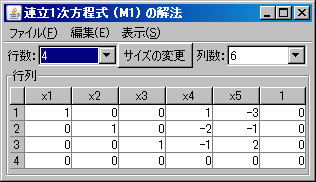
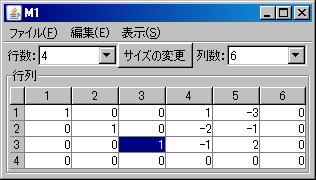
例として、同次方程式 $ \left\{ \begin{array}{cccccc} x_1 & -x_2 & +2x_3 & + x_4 & +2x_5 & =0 \\ & x_2 & +x_3 & -3x_4 & +x_5 & =0 \\ 3x_1 & -4x_2 & +7x_3 & +4x_4 & +9x_5 & =0 \\ x_1 & + 2x_2 & +x_3 & -4x_4 & -3x_5 & =0 \end{array} \right. $ を解く。必要ならば、「行列の新規作成」ボタンを押し、行列を作成する。右辺の定数列も含めるので、解きたい連立1次方程式の大きさは4行6列である。（ここでは、M1という名前がついている。）

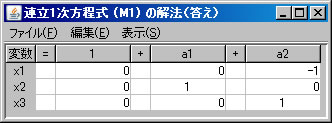
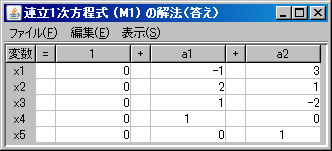
「行列の演算」ウィンドウに戻り、「行列A」リストボックスでM1を選択し、「連立1次方程式(A)の解法」ボタンを押すと、「連立1次方程式(M1)の解法」ウィンドウに答えが表示される。

「表示」メニューから「解の表示」を選ぶと、

のように、答えが陽に表示される。

ピボット操作1

上記の同次連立1次方程式（M1）をピボット操作を利用して解く。「行列の演算」ウィンドウに戻り、「行列A」リストボックスでM1が選択されていることを確認する。（解く経過を残さない場合は、「結果を新ウィンドウに表示」のチェックを外す。）

1行1列の要素「1」をクリックし、選択し、

「行列の演算」ウィンドウの「ピボット操作」ボタンを押す。

2行2列の要素「1」を選び、

「ピボット操作」ボタンを押す。

3行3列の要素「2」を選び、

「ピボット操作」ボタンを押す。

となり、答えが得られた。

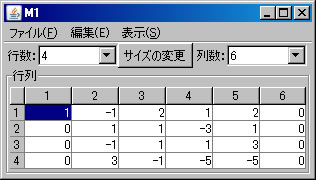
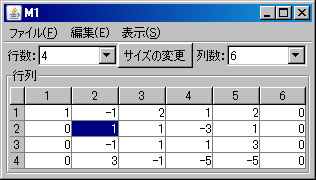
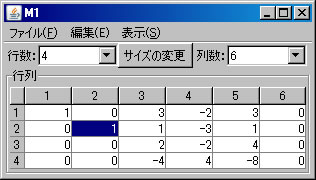
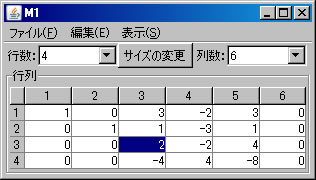
非同次連立1次方程式

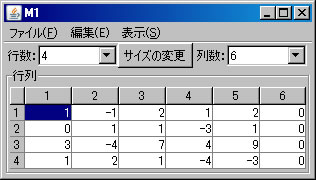
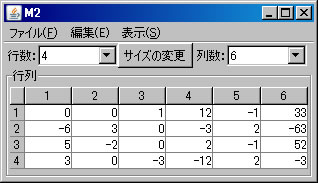
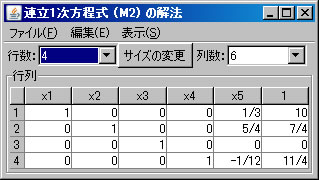
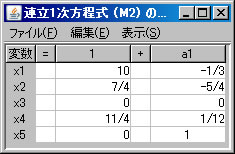
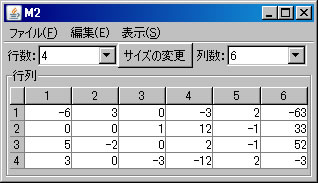
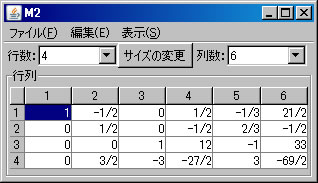
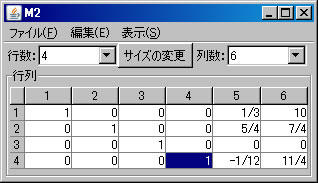
例として非同次連立1次方程式 $\left\{ \begin{array}{cccccc} & & x_3 & +12x_4 & -x_5 & =33 \\ -6x_1 & +3x_2 & & -3x_4 & +2x_5 & =-63 \\ 5x_1 & -2x_2 & & +2x_4 & -x_5 & =52 \\ 3x_1 & & -3x_3 & -12x_4 & +2x_5 & =-3 \end{array} \right. $ を解く。必要ならば、「行列の新規作成」ボタンを押し、行列を作成する。解きたい連立1次方程式の大きさは4行6列（右辺の定数列も含める）なので、列数を「6」に変更し、「サイズの変更」ボタンを押し、データを入力する。（ここでは、M2という名前がついている。）「行列の演算」ウィンドウに戻り、「行列A」リストボックスでM2を選択し、「連立1次方程式(A)の解法」ボタンを押すと、「連立1次方程式(M2)の解法」ウィンドウに答えが表示される。

「表示」メニューから「解の表示」を選ぶと、

のように、答えが陽に表示される。

ピボット操作2

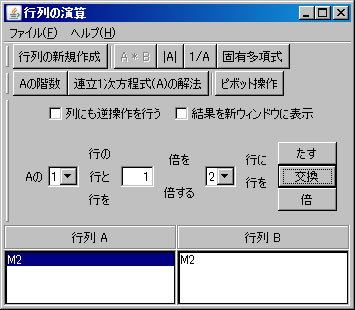
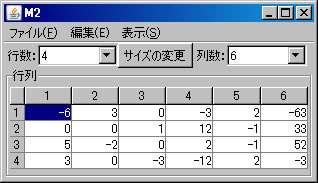
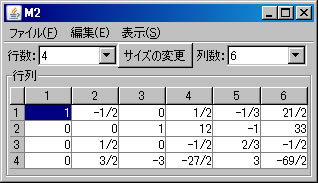
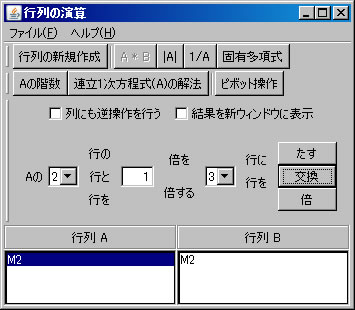
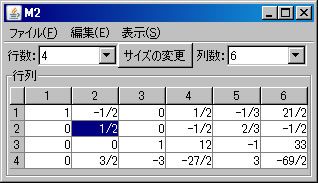
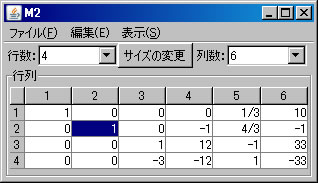
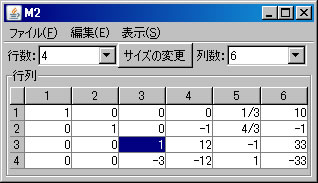
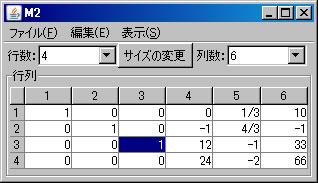
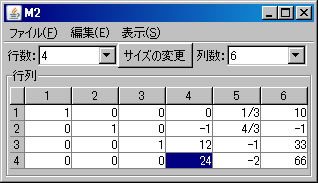
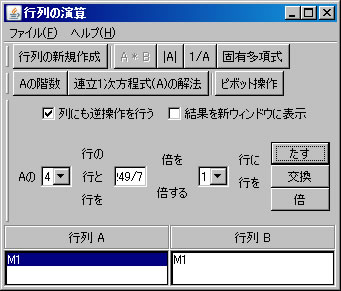
上記の非同次連立1次方程式（M2）をピボット操作を利用して解く。「行列の演算」ウィンドウに戻り、「行列A」リストボックスでM2が選択されていることを確認する。（解く経過を残さない場合は、「結果を新ウィンドウに表示」のチェックを外す。）1行と2行を交換するために、「1」と「2」を選び、「交換」ボタンを押す。

1行１列の要素「-6」をクリックし、選択し、

「行列の演算」ウィンドウの「ピボット操作」ボタンを押す。

2行と3行を交換するために、「2」と「3」を選び、「交換」ボタンを押す。

2行2列の要素「1/2」を選び、

「ピボット操作」ボタンを押す。

3行3列の要素「1」を選び、

「ピボット操作」ボタンを押す。

4行4列の要素「24」を選び、

「ピボット操作」ボタンを押す。

となり、答えが得られた。

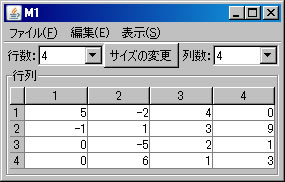
逆行列

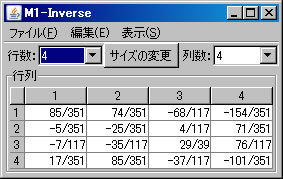
例として $\left( \begin{array}{cccc} 5 & -2 & 4 & 0 \\ -1 & 1 & 3 & 9 \\ 0 & -5 & 2 & 1 \\ 0 & 6 & 1 & 3 \end{array} \right)$ の逆行列を求める。必要ならば、「行列の新規作成」ボタンを押し、この行列を作成する。（ここではM1という名前がついている。）「行列の演算」ウィンドウに戻り、「行列A」リストボックスにおいて、M1を選択し、「1/A」ボタンを押す。新しいウィンドウに逆行列M1-Inverseが表示される。

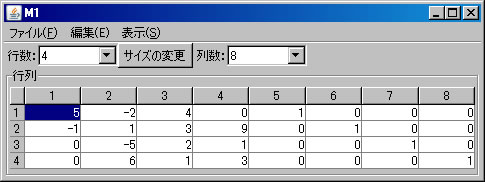
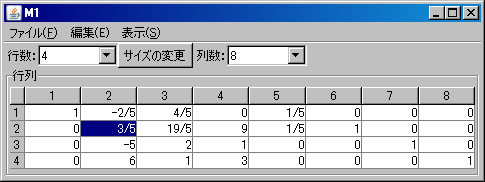
次に、「ピボット操作」を利用して逆行列を求める。上記のM1の列数を「8」に変更し、5列目から8列目までに単位行列を入力する。（解く経過を残さない場合は、「結果を新ウィンドウに表示」のチェックを外す。）1行1列の要素「5」を選択し、

「ピボット操作」ボタンを押す。2行2列の要素「3/5」を選択し、

「ピボット操作」ボタンを押す。3行3列の要素「101/3」を選択し、

「ピボット操作」ボタンを押す。4行4列の要素「-351/101」を選択し、

「ピボット操作」ボタンを押す。

5列目から8列目までに逆行列が求まっている。

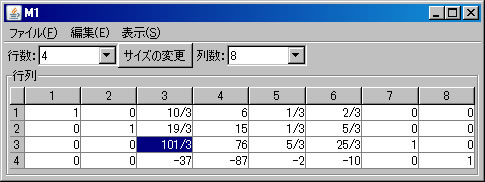
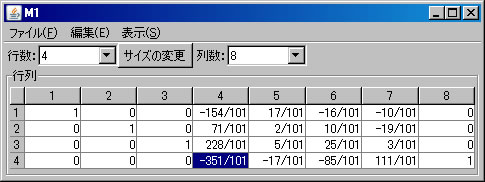
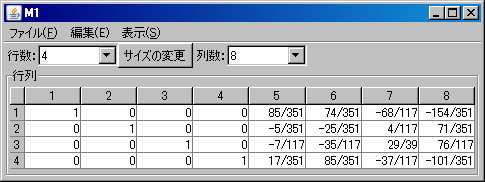
行列式

例として行列式 $ \left| \begin{array}{cccc} 5 & -2 & 4 & 0 \\ -1 & 1 & 3 & 9 \\ 0 & -5 & 2 & 1 \\ 0 & 6 & 1 & 3 \end{array} \right| $ を求める。必要ならば、「行列の新規作成」ボタンを押し、この行列を作成する。（ここではM1という名前がついている。）「行列の演算」ウィンドウに戻り、「行列A」リストボックスで、M1を選択し、「|A|」ボタンを押す。結果が、新しいウィンドウに表示される。ステータスバーを見れば行列式が-351であることがかる。

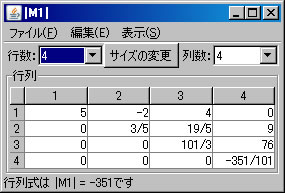
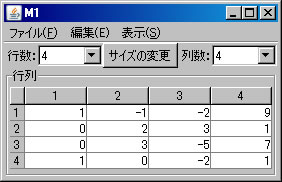
固有多項式

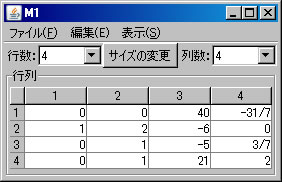
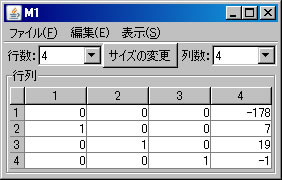
例として $ \left( \begin{array}{cccc} 1 & -1 & -2 & 9 \\ 0 & 2 & 3 & 1 \\ 0 & 3 & -5 & 7 \\ 1 & 0 & -2 & 1 \end{array} \right)$ の固有多項式を求める。必要ならば、「行列の新規作成」ボタンを押し、この行列を作成する。（ここではM1という名前がついている。）「行列の演算」ウィンドウに戻り、「行列A」リストボックスにおいて、M1を選択し、「固有多項式」ボタンを押す。新しいウィンドウに固有多項式を容易に求めることができる行列M1-CharFunが表示される。

この行列から、固有多項式が $ \lambda^4 + \lambda^3 – 19\lambda^2 – 7\lambda + 178 $ であることが分かる。

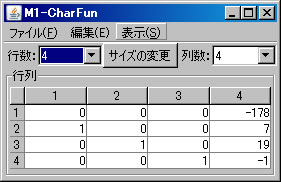
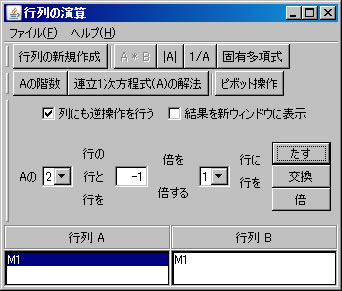
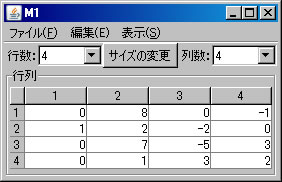
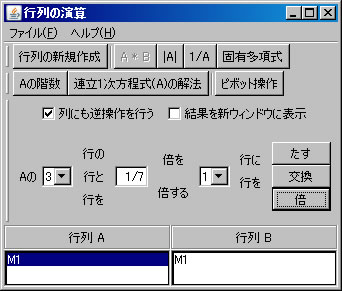
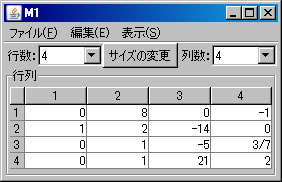
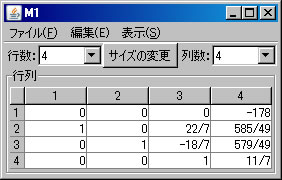
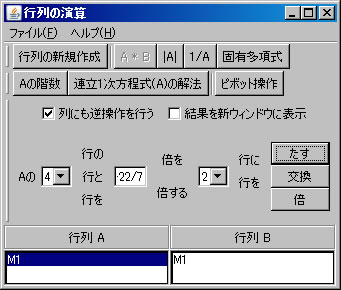
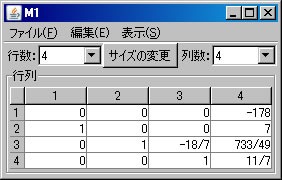
次に、行列の基本変形を利用して行列M1の固有多項式求める。（利用する計算方法についてはテキストを参照すること。）「行列の演算」ウィンドウに戻り、「行列A」リストボックスでM1を選択する。「列にも逆操作を行う」をチェックする。（解く経過を残さない場合は、「結果を新ウィンドウに表示」のチェックを外す。）2行と4行を交換するために、「交換」ボタンを押す。

2行の-1倍を1行に加える

3行を1/7倍する

3行の-8倍を1行に加える

3行の-2倍を2行に加える

3行の-1倍を4行に加える

4行を7/193倍する

4行の-249/7倍を1行に加える

4行の-22/7倍を2行に加える

4行の18/7倍を3行に加える

となり、同じ答えが得られた。

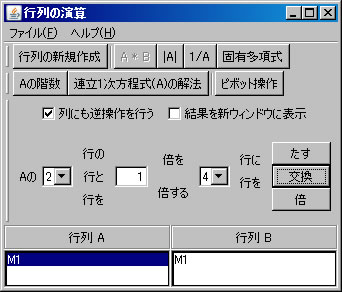
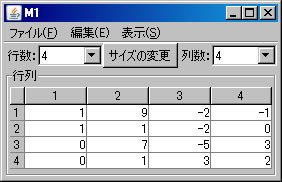
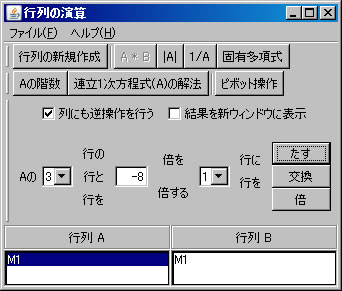
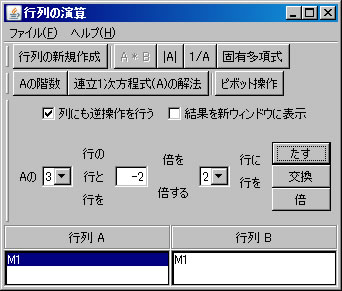
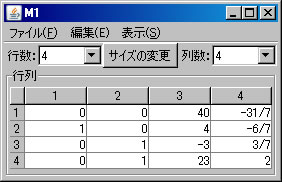
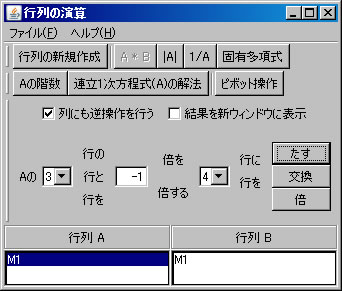
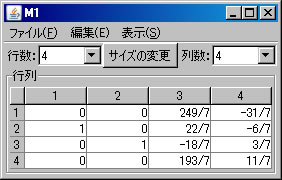
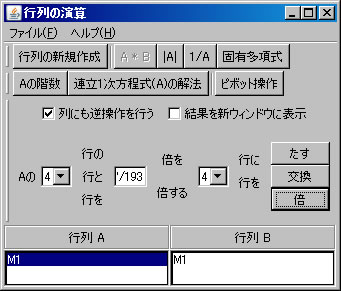
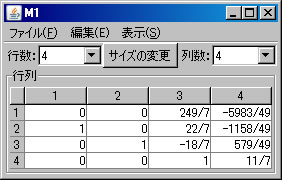
固有値と固有ベクトル

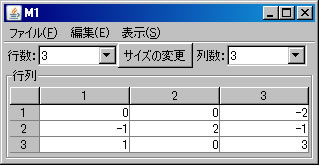
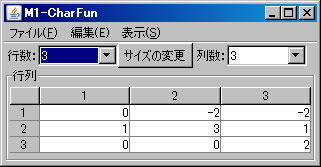
例として $A=\left( \begin{array}{ccc} 0 & 0 & -2 \\ -1 & 2 & -1 \\ 1 & 0 & 3 \end{array} \right)$ の固有値と固有ベクトルを求める。必要ならば、「行列の新規作成」ボタンを押し、サイズを3行3列に変更し、この行列を作成する。（ここではM1という名前がついている。）「行列の演算」ウィンドウに戻り、「行列A」リストボックスにおいて、M1を選択し、「固有多項式」ボタンを押す。新しいウィンドウに固有多項式を容易に求めることができる行列M1-CharFunが表示される。

$ \left( \begin{array}{cc|c} 0 & -2 & -2 \\ 1 & 3 & 1 \\ \hline 0 & 0 & 2 \end{array} \right) $

左上の2次の行列より $ \lambda^2 – 3\lambda + 2 $ が右下の1次の行列より $ \lambda – 2 $ が得られ、結局、$A$ の固有多項式は \[ f_A(\lambda)=\left| \begin{array}{ccc} \lambda & 0 & 2 \\ 1 & \lambda – 2 & 1 \\ -1 & 0 & \lambda – 3 \end{array} \right| = \left( \lambda^2 – 3\lambda + 2 \right) \left( \lambda – 2 \right) = \left( \lambda – 1 \right) \left( \lambda – 2 \right)^2 \] となる。これより固有値は1と2（2重解）となる。

固有値1に属する固有ベクトルは、係数行列が上記の固有多項式 $f_A(\lambda)$ の行列式の部分（ $\lambda = 1$ とおく）である、次の同次連立方程式の解である。 \[ \left\{ \begin{array}{cccc} x_1 & & +2x_3 & =0 \\ x_1 & -x_2 & +x_3 & =0 \\ -x_1 & & -2x_3 & =0 \end{array} \right. \]

必要ならば、「行列の新規作成」ボタンを押し、サイズを3行4列に変更し、この行列を作成する。（ここではM1という名前がついている。）「行列の演算」ウィンドウに戻り、「行列A」リストボックスでM1を選択し、「連立1次方程式(A)の解法」ボタンを押すと、「連立1次方程式(M1)の解法」ウィンドウに答えが表示される。さらに、「表示」メニューから「解の表示」を選ぶと、

となり、固有値1に属する固有ベクトルは $ \alpha \left( \begin{array}{c} -2 \\ -1 \\ 1 \end{array} \right) $ となる。

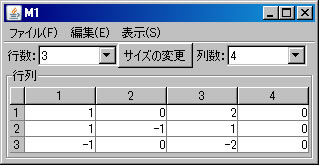
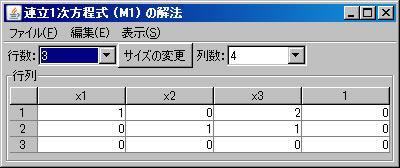
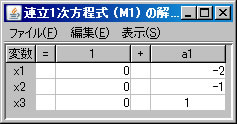
同様に、固有値2に属する固有ベクトルは、係数行列が上記の固有多項式 $f_A(\lambda)$ の行列式の部分（ $\lambda = 2$ とおく）である、次の同次連立方程式の解である。 $$ \left\{ \begin{array}{cccc} 2x_1 & & +2x_3 & =0 \\ x_1 & & +x_3 & =0 \\ -x_1 & & -x_3 & =0 \end{array} \right. $$ 必要ならば、「行列の新規作成」ボタンを押し、サイズを3行4列に変更し、この行列を作成する。（ここではM1という名前がついている。）「行列の演算」ウィンドウに戻り、「行列A」リストボックスでM1を選択し、「連立1次方程式(A)の解法」ボタンを押すと、「連立1次方程式(M1)の解法」ウィンドウに答えが表示される。さらに、「表示」メニューから「解の表示」を選ぶと、

となり、固有値2に属する固有ベクトルは $ \beta \left( \begin{array}{c} 0 \\ 1 \\ 0 \end{array} \right) + \gamma \left( \begin{array}{c} -1 \\ 0 \\ 1 \end{array} \right) $ となる。